基于AOA的多功能n-1阶电流模式滤波器

关键字： 输入 电阻 差动 放大

已有文献报道了电流模式n阶CCCII(±)-低通滤波器的系统设计，这种设计方法思路清晰，数学简便。然而，由于CCII(second generation currentconveyor)、CCC II (second generation currentcontrolled conveyor)的Y端高阻抗，不仅使以它为有源器件的积分器易受寄生电容影响，误差大，而且使反馈网络有不可忽视的正向传输，使得理论分析误差大；此外，CCCII的X端寄生电阻与温度成正比，致使滤波器参数温度的稳定性差。为此，笔者用AOA有源器件代替CCC II，因AOA输入端“虚地”，从而解决了因使用CCCII所带来的问题，并通过巧妙设计，获得了低通、高通和两种带通滤波功能。

1 AOA及其基本电路模块

AOA的电路符号如图1(a)所示。当AOA为理想情况下，则μ=∞，Ii=Io-／μ=Io+／μ。当引入负反馈后，AOA是输入端“虚地”、“虚断”，输出电阻为无穷大，电流增益亦为无穷大的差动输出理想电流放大器。

由AOA构成的多路输出积分器如图1(b)所示。由图知：

可见这是有两个输出的电流模式的反相积分器。因输入端“虚地”，积分器的时间常数较少受寄生电容的影响，故该积分器精度高。

由AOA构成的多路输出比例电路如图1(c)所示。其反相输出为：

2 AOA多功能n-1阶电流模式滤波器

由n-1个AOA两输出反相积分器和一个AOA多路输出比例电路构成的多功能n-1阶电流模式滤波器如图2所示。

式中：Io=[Io1，Io2， …Ion]T，If=[If1，If2， …Ifn]T。为保证积分器的关系成立，其输出端需“虚地”，因此反馈网络的输入Io与输出If应短接，则有Fij=-1。

考虑到反馈网络只有反相传输，在i>j时，必有Fij=0，所以F为一上三角阵。再考虑到只引入负反馈，当i为奇数，j为偶数；或者当i为偶数，j为奇数时，应有Fij=0。则反馈网络矩阵为

根据AOA积分器的端口特性，可列出电流方程组(7)，其中τi=RiCi，i=1，2，…，n-1，k=Rn／Rn’。由式(6)、(7)得式(8)，其中Ii=[Ii1，Ii2，…，Iin]T为输入电流向量，Io=[Io1，Io2， …，Ion]T为输出电流向量。滤波器的系统矩阵A(s)为式(9)。

其中|A(s)|为矩阵A(s)的系数行列式，A*(s)为A(s)的伴随矩阵。

若Io=Ion，解式(10)得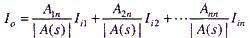

其中Aij表示A中各元素在A中的代数余子式。从而得到多输入、单输出多功能滤波器。

若Ii=Iin，Ii1=Ii2=…=Iin-1=0，解式(10)得

从而得到单输入、多输出多功能滤波器。

3 设计实例

为运算简单，以三阶多输入、单输出多功能巴特沃思滤波器为例进行说明。由式(9)得三阶滤波器的系统矩阵为：

为获得低通、带通、高通输出，令f11=f22=f33=f44=f13=0，则有

其中

为使系统稳定、简单，选取k=1，f34=1，f14=1，f24=-1。若取τ1τ2τ3=1，τ1τ2=2，τ1=2，则τ2=1，τ3=0.5，即为三阶巴特沃思滤波器。如图3所示。

若Ii=Ii1，Ii2=Ii3=Ii4=0，则有

Io／Ii=1／s3+2s2+2s+1

实现了三阶巴特沃思低通滤波。

若Ii=Ii2，Ii1=Ii3=Ii4=0，则有

Io／Ii=-2s／s3+2s2+2s+1

实现了三阶巴特沃思带通滤波。

若Ii=Ii3，Ii1=Ii2=Ii4=0，则有

Io／Ii=2s2／s3+2s2+2s+1

实现了三阶巴特沃思带通滤波。

若Ii=Ii4，Ii1=Ii2=Ii3=0，则有

Io／Ii=-s3／s3+2s2+2s+1

实现了三阶巴特沃思高通通滤波。

4 计算机仿真

在图3中，取τ1τ2τ3=1，τ1τ2=2，τ1=2，则τ2=1，τ3=0.5即为三阶巴特沃思滤波器。设截止频率为105rad／s，若取R=10 kΩ，则去归一化后电容值为C1=2 nF，C2=1 nF，G3=0.5 nF。具体仿真时，先将AOA按文[10]给出的双极型电路实现，然后创建其子电路。再按图3电路进行仿真。为了能用EWB软件仿真电流模电路，考虑到AOA端“虚地”，故可用电压源串联10 kΩ电阻等效电流源Ii，则输入、输出电压除以10 kΩ即代表输入、输出电流(单位是mA)，从而实现电流模电路仿真。结果如图4所示，其中曲线(1)代表单位输入电流(1 mA)，(a)、(b)、(c)、(d)中曲线(2)分别为低通、带通、带通、高通电流增益，可见与理论分析一致。

5 结论

提出了一种设计AOA多功能高阶电流模滤波器的系统方法，该滤波器可在同一端口分别实现多种滤波功能，也可在不同端口同时实现多功能滤波。与CCCII(±)高阶低通电流模式滤波器相比，其最大特点是理论误差小，精度高；滤波器参数取决于无源电阻、电容，与温度无关，因而稳定性好。这对VLSI单片集成技术，有着重要的参考作用。

相关阅读

编辑：

本文引用地址： https://www.eeworld.com.cn/designarticles/analog/200712/17354.html

[发表评论]

[加入收藏]

[告诉好友]

[打印本页]

[关闭窗口]

[返回顶部]

[RSS订阅]