振动筒式压力传感器的FLANN非线性校正

     摘要：采用函数链神经网络方法对振动筒式压力传感器进行非线性校正，与BP算法相比，函数链神经网络结构明了、算法简单、易于收敛。文中介绍了函数链神经网络解决振动筒式压力传感器的非线性原理和建模方法，仿真实验结果证明了该方法的可行性和有效性。

关键词：函数链神经网络，非线性，振动筒

0 引言

  传感器的非线性校正有多种方法，并且也都得到了不同程度的应用。传统的非线性传感器线性化的方法是硬件补偿，这种方法难以做到全程补偿，而且补偿硬件的漂移会影响整个系统的精度，因此可靠性不高、测量范围有限、精度低。现在国内外研究人员研究了多种多项式拟合校正法，当用直线拟合时，拟合精度较低，通常不能满足要求；用高次曲线拟合又过于复杂，实现困难。近年来发展较多的是神经网络法，大都采用的是BP算法［1］［2］。在理论上，含有隐含层的BP网络能够逼近任意的非线性函数，这种方法适应性强，精度也高。但是BP网络结构复杂、调节的权值多、学习速度慢、容易陷入局部最小。为此本文采用了一种基于函数链神经网络（FLANN）的传感器线性校正方法，与BP算法相比，该结构简单明了。通过在振动筒式压力传感器的上仿真实验证明，该方法简单易行，效果理想。

1 振动筒式压力传感器

  振动筒式传感器是利用弹性元件的振动频率随被测力而变化实现测量的。振动筒是传感器的敏感元件，当被测压力通过圆筒内腔时，由于被测压力的作用，沿轴向和径向被张紧的振动筒的刚度发生变化，从而改变了振动筒的谐振频率。频率变化值对应着压力变化的大小，振动频率f与被测压力P的关系为：    式中，A—振动筒常数，它与振动筒材料性质和振动几何尺寸有关[3]。振动筒式压力传感器工作  

  在不同的环境温度条件下，随着环境温度的变化，其测量误差也会不同。另外振动筒金属材料的弹性模量也随温度变化而变化，温度变化将会造成筒内气压不稳定。这些因素都直接影响着振动筒频率变化与压力大小的线性关系。在测量中等压力时，其非线性一般在5－6％。所以在精度要求较高的场合，必须对振动筒式压力传感器进行线性校正。

2 非线性校正原理

  非线性校正的原理主要基于图1所示的基本环节，图中输出函数y主要由振动筒式压力传感器的特性决定。由于温度等因素的影响，其线性度差，因此y和u是非线性关系。如果校正函数F具有与f相反的变换特性，即 p= F ( y ) = f ( u )－1，那么校正后的输出p与输入u就可以成为较理想的线性关系。所以问题的关键是如何确定校正函数F，在实际应用中很难准确求出该校正函数即其反函数，为此引入了函数链神经网络算法。

由回归分析法，可以知道函数F可以用下列多项式近似地表示：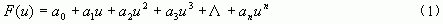

式中：n为多项式的阶数，它越大式（1）就越接近真实的校正函数F，其校正结果也越精确。在实际中n越大，式（1）的an un项将会急剧减小，因此n也不必取得太大。当n确定后，下面的问题就是如何确定各项的系数，文中重点介绍了使用函数链神经网络法对各项系数的确定。

3 函数链神经网络的建模

采用函数链神经网络进行振动筒式压力传感器校正的模型如图2所示。

图2 函数链神经网络模型图

图中：，为训练样本的输入元素它对应式（1）中的1，u，u2，u3，…，un；Wj（j＝0，1，2，…，n）为网络的连接权，它用来确定式（1）中的待定系数a0，a1，a2，…，a n；di为传感器的标定周期（频率的倒数）值。在该神经网络中，每个神经元都采用线性函数，因此函数链神经网络的输出为：

（2）

式中：P（k）为第k步时，di的估计值，它与di比较，得到第k步的估计误差：

  （3）

然后根据式（4）调节神经网络的连接权值：

 （4）

式中：wj（k+1）为第k步时，第j个连接权值，是学习因子。在进行神经网络算法之前，先通过振动筒标定实验获得多组输入输出标定值对（Xi，di），Xi为压力值。标定点要分布在整个测量范围之内。另外还要对Xi进行归一化到[－1，＋1]，即xi＝Xi / Xmax，Xmax为Xi的最大绝对值。其整个算法过程如下：

（1）       确定函数链神经网络结构。

（2）       网络连接权值初始化，随即设定wj，一般wj的初始值取[－1，1]之间的随机数。

（3）       输入训练数据样本xi，di。

（4）       由式（2）计算P（k）

（5）       由式（3）计算误差ei( k )。如果误差满足要求则转到（7），否则继续。

（6）       由式（4）修正wj（k），调节权值，返回（4）。

（7）       误差ei( k )达到最小，学习过程结束。得到最终的权值w0，w1，…，wn。

  学习过程中还要注意学习因子的取值，它的选择会影响到迭代稳定性和收敛速度。大则收敛速度快，但稳定性不好；反之，则稳定性好，但是收敛速度慢。

4振动筒压力传感器的非线性校正

  对飞行器进行气压检测是航空部门必不可少的，气压的检测一般都是采用的振动筒式压力传感器。表1是以某振动筒压力传感器对飞行器气压在温度为20℃时的部分压力标定值，将它们归一化后作为神经网络的输入样本数据。在训练时对应某个温度值就有相应的25个样本数据，在训练中分别选取了温度为－40℃、－20℃、－10℃、0℃、10℃、40℃、60℃等不同范围进行训练学习。

表1 传感器在温度20℃时的部分压力标定值数据

压力mmHg	172.295	197.183	203.625	210.804	218.798	227.800	232.745	237.481
周 期	2000	1000	800	600	400	200	100	10

 

  在实验过程采用较为流行的MATLAB软件进行仿真。初始化中，学习因子取值为1.1，误差e取值0.00035，n＝3。经过多次迭代，不断调节网络的连接权值，最终求出权值，确定了式（1）中多项式的系数为：a0＝237.6144，a1＝－54.1649，a2＝2.9464，a3＝0.001129。所以该振动筒压力传感器的校正函数为：

（5）  

表2传感器在温度20℃时的部分压力计算值与标定值的比较

压力mmHg	172.425	197.255	203.682	210.711	218.858	227.891	232.798	237.375
周 期	2000	1000	800	600	400	200	100	10

  根据所得以上函数，对－40℃～60℃范围内8个温度点的标定值和由方程式（5）所得的估计值进行了比较。在表2中列出了温度在20℃时的估计值，和表1比较可知该模型的精度较高。其最大相对误差小于0.08%，完全可以满足大多数工程允许的误差，以实现压力非线性校正。

5结论

  使用函数链神经网络进行振动筒式压力传感器非线性校正具有结构简单、自学习能力强、易于收敛、效果良好的特点。它的训练的确比BP算法容易，而且算法也简单得多；是一种很好的非线性校正方法，它也可以完全用于其他类型传感器的非线性校正。