在控制领域中,PID控制足最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛应用于工业过程控制。此外,随着控制理论的发展,专家系统、模糊逻辑、神经网络、灰色系统理论和传统的PID控制策略相结合又派生出各种新型的PID类控制器,形成庞大的PID家族,很多算法大大改进了传统P1D控制器的性能。然而,这些算法在工业中的实际应用范围却远远落后于传统PID算法,其中一个原因就足传统的单片机加分立元件构成的工业控制系统在实施更新更复杂的算法时,算法的复杂性或使得系统硬件设计调试更加复杂,或使得单片机内软件代码行增多,延时加大,开发周期变长。稳定性和可靠性在新系统设计时成为不能忽视的一个问题。
而近年来,微电子技术的迅速发展,使得集成电路设计和工艺水平有了很大的提高,随着超深亚微米技术的发展,使得原先由许多IC组成的电子系统集成在一个单片硅片上成为可能,构成所谓的片上系统(System 0n Chip,SOC),同时也促进了相应EDA工具的蓬勃发展。
控制算法的极大丰富和微电子领域工艺技术及EDA工具的飞速发展,使得我们可以将两个领域的应用优势集合在一起,在EDA工具的帮助下便捷快速地在FPGA上可靠地实现各种新型算法,完成整个控制系统从行为算法级(系统级)到物理结构级的全部设计,从而达到将各种新型PID算法广泛应用于实际工业控制系统的目标。
2离散PID控制算法
2.1 PID算法
比例、积分、微分(PID)控制是控制系统中技术最成熟,运用最广泛的一种控制方式。其基本原理是根据反馈控制系统的偏差值按比例、积分、微分函数关系进行运算,所得结果输出给执行机构,执行机构根据偏差值的运算结果来控制被控对象。在连续时间域中,PID控制器算法的表达式为:
其中:e(t)为控制器的输入即控制系统的给定量与输出量的偏差;u(t)为控制器的输出;Kp为比例系数;Tl为积分时间常数;TD为微分时间常数。
2.2 PID算法的离散化
由于计算机控制只能根据采样时刻的偏差值计算控制量,因此需对上式进行离散化处理。按模拟PID控制算法式(1),以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分(和式)近似代替积分,以一阶向后差分(增量)近似代替微分,即: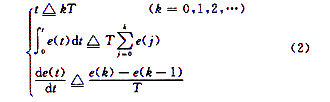
可得离散PID表达式:
式中,积分系数K1=KP/Tl,微分系数KD=KPTD,T为采样周期,k为采样序号,k=1,2,…,e(k一1)和e(k)分别为第(k一1)和第k时刻所得的偏差信号。
2.3 PID控制系统框图
一般控制系统的PID系统控制框图如图1所示。其中,source为系统设定值,feedback为系统反馈值,e(t)为反馈误差,u(t)为PID控制器输出值。图中"PID控制算法"框图子系统即需要我们在算法级用DSP Builder进行自顶向下的设计仿真。

3基于DSP Builder的PID控制系统FPGA设计步骤与开发
3.1 Simulink工具箱的A1tera DSP Builder 组件
在利用FPGA进行系统的开发应用上,已有了全新的设计工具和设计流程。DSP Builder。就是Altera公司推出的一个面向DSP之类的芯片级开发的系统级工具。他是作为Matlab的一个Simulink工具箱(Tool Box)出现的,他使得用FPGA设计专用芯片系统完全可以通过Simulink的图形化界面进行,只要简单地对DSP Builder工具箱中的模块进行调用即可。值得注意的是,DSP Builder中的基本模块是以算法级的描述出现的,易于用户从系统或者算法级进行理解,甚至不需要十分了解FPGA本身和硬件描述语言。这为传统控制系统领域的工程师开发基于FPGA/ASIC的可靠控制系统芯片自顶向下的算法级设计提供了便利的条件。
3.2 在Matlab中用DSP Builder完成顶层算法设计
设计方法可以从与硬件完全无关的系统级开始,首先利用Matlab强大的系统设计、分析能力和DSP Builder提供的模块(或IP核)完成顶层系统设计及系统仿真测试。
根据图1的原理,在Matlab中进行设计仿真,Simulink顶层设计模型如图2所示。
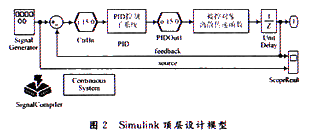
在顶层设计模型中,除"PID控制子系统"外,其他部分均采用一般Simulink组件设计。为了在验证仿真时更贴近实际系统,给被控对象加上可调延时深度的延时即节。信号发生器给出系统设定值,对一般实际应用的控制系统而言,可以使用典型的矩形波,这里用数个矩形波与正弦波的叠加来仿真系统设定值的给出。
模型中的"PID控制子系统"实现PID算法部分。该子系统经仿真设计后,将通过DSP Builder中的SignalCompiler转换为FPGA的HDL 语言设计,所以这部分除了仿真观察所需的示波器等外需全部采用DSP Builder组件来设计,否则Signal Compiler编译时不能识别。
为了简单地说明如何用DSP Builder自顶向下的设计基于FPGA的控制系统,这里用普通的位置式PID算法进行举例。位置式PID算法的PID控制子系统设计框图如图3所示。

在图3中,输入误差信号采用了16位精度。而为了实现比例、积分、微分系数的精确可调,在这里PID系数采用了8位精度,使系数至少可以精确到百分位。同时,在系统设计过程中为了尽量避免浮点数的运算,这里将PID系数取成整型,先放大数据值到24位,而在并行加法器运算单元后用IO&Bus中的总线转换器单元对累加后的数据进行位数转换,实现FPGA中的浮点数运算。
Matlab仿真结果如图4所示。其中,source为系统设定值,feedback为系统反馈值。

波形仿真成功后,需要将Matlab中图形化的顶层设计模型转换成能够被FPGA开发软件识别的HDL语言描述文件。在图2中,打开Signal Compiler模块,配置相关参数,可以将DSP Builder 设计的"PID控制子系统"编译成VHDL及Veirlog语言的RTL表述和工具命令语言Tcl脚本。根据编译信息前面的设计模型,直到编译报告中Convert Mdl to VHDL,Synthesis,Quartus II Fitter三项状态均为PASSED,即可获得ModelSim所需的tb_SystemName.tcl功能仿真文件脚本和Quartus所需的SystemName.qpf 项目文件和SystemName.vec 仿真波形文件。
3.3在ModelSim中实现HDL代码功能仿真
在ModelSim菜单中执行Tools一>Execute Macro,打开前述Signal Compiler编译生成文件tb_System-Name.tcl(VHBL)或tb_vo_SystemName.tcl(Verilog),调试成功后,仿真得到图5结果。功能仿真结果与Matlab中基本一致,证明顶层设计基本成功。
3.4 在Quartus中实现FPGA开发
在Quartus中打开前述Signal Compiler编译生成文件SystemName.qpf。设定相应器件Device,在Tcl Scripts中运行SystemName_quartus.tcl配置此工程项目变量,然后编译。调试成功后,载入SystemName.vec波形仿真文件运行时序仿真工具,得到图6结果,与图5基本相符,证明设计成功。


4结 语
这里给出了一个最初用于FPGA的系统级设计工具DSP Builder在自动控制领域的应用,目前在已出版的国内期刊及论文库中似乎还没有相关文献谈到这个交叉领域的应用。
在控制领域里,当各种复杂的新型PID算法应用于实际控制系统中时,由于传统单片机与分立元件电路系统的局限性,硬件指标和软件复杂度都使得新的应用及研发设计进展缓慢;普通FPGA/CPLD没计又存在着没计周期长、可重复利用性差等缺点。我们将日益完善的SoC设计工具应用于自动控制领域,不仅在算法设计上有了新的方便快捷的设计工具,同时籍由FPGA硬件本身的优点也可以解决单片机及分立元件存在的电磁干扰、系统复杂度高等各类问题,从而大大提高将各种新型PID算法广泛应用于实际工业控制系统的可行性。
在系统设计中进一步的探讨:由于设计是从与硬件完全无关的Matlab系统级仿真开始,因此便于传统控制领域工程师们可以迅速地将算法级的构思应用于控制系统设计中,从而可以将有限的精力专注于系统级算法的设计,而避免陷入重复繁琐的电路设计中去,缩短从人脑构思到实际系统实现的时间周期。其中单个设计MDL文件甚至可以考虑封装成"算法包"的形式进行资源重复利用,以实现功能单元的便捷增减和缩短产品开发时间。这里可能存在着控制领域里可重用算法及相应"包"的接口标准。这种情况或许和SOC领域IP核的现象有部分类似,本文就不再多述。
上一篇:基于ARM微处理器LPC2132的智能电动机保护器设计
下一篇:基于处理器的去方块滤波器的实现及优化
推荐阅读最新更新时间:2024-03-30 21:24




 机器视觉技术及应用 (韩九强, 胡怀中)
机器视觉技术及应用 (韩九强, 胡怀中) Verilog HDL数字集成电路设计原理与应用
Verilog HDL数字集成电路设计原理与应用









 京公网安备 11010802033920号
京公网安备 11010802033920号