在微机化的仪器仪表控制软件中,特别是快速控制软件中,或因直接计算过于复杂,或因只有经验数据没有理论公式,常采用查表插值法计算某些数据。
一般适合于插值法的函数是光滑性较好的函数。所谓“光滑性较好”是指以下两个方面:
◆连续且尽量高阶地可导:
◆其泰勒展开式中高次项的绝对值较小。
采用多项式插值时,若提高多项式次数,除了增加计算量(在高速实时控制的程序中,计算速度是很重要的问题)外,从数学上看还有若干缺点,故实际应用中一般不用太高的次数。抛物线插值(三点二次插值)是常用的一种。
提高精度的另一途径是增加节点密度。对于三点二次插值,节点密度若能提高二倍,则截断误差大约可以缩小到原来的1/8。但是这样一来数据表的容量也要加大二倍,因此在容量和精度间存在着矛盾。
本文介绍一种“四点二次插值”算法,与普通三点=次插值相比,节点密度不变,计算量也差不多,但精度(最大误差限)大致相当于节点密度提高二倍的效果。
四点二次插值的思想是:计算(xk,xk+1)区间的插值时,用(xk-1,xk,)的三点二次插值结果和(xk,xk+1)的三点二次插值结果相平均,作为最后结果。若采用等距节点,间距为h,根据这个思想,不难推出以下计算公式:
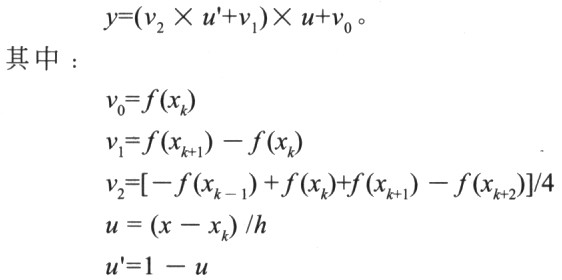 与普通的三点二次插值法对比,可以看出计算量差不多(乘法次数相同,除以4可以用移位实现)。
下面粗略分析其精度。
二次插值误差余项应有三个零点,此法中xk和k+1是其两个零点。显然,如果第三个零点在x1和xk+1的中点处,则其精度和节点密度提高二倍后的三点二次插值法相同。
设(xk-1,xk,xk+1)的三点二次插值误差余项为R1(x),(xk,xk+1xk+2)的三点二次插值误差余项为R2(x)则四点二次插值的误差余项为
与普通的三点二次插值法对比,可以看出计算量差不多(乘法次数相同,除以4可以用移位实现)。
下面粗略分析其精度。
二次插值误差余项应有三个零点,此法中xk和k+1是其两个零点。显然,如果第三个零点在x1和xk+1的中点处,则其精度和节点密度提高二倍后的三点二次插值法相同。
设(xk-1,xk,xk+1)的三点二次插值误差余项为R1(x),(xk,xk+1xk+2)的三点二次插值误差余项为R2(x)则四点二次插值的误差余项为
 系数K(ξ1′,ξ2)反映中点xm处四点二次插值的误差,比原来三点二次插值的误差减小的程度。若f"""(x)是常数,则k(ξ1,ξ2)=0,因而R(xm)=0。也就是说,R(z)第三个零点在xm处,达到上文所述的效果。
对于比较光滑的函数,f"""(x)在小区间内不会变化太大,故k(ξ1,ξ2)式中的分子绝对值应较小。若K(ξ1,ξ2)近于0,则R(xm)也近于0,R(x)的零点仍在xm附近,效果与上述接近。可以证明(限于篇幅.证明略),只要f"""(ξ1)与f"""(ξ)之比在O.5~2之间,则第三个零点必然在xk和xk+1之间。
若K(ξ1,)绝对值较大即f"""(ξ2)与f"""(ξ2)之比距1较远),或,f"""(ξ1)与,f…(ξ2)反号,则零点不在中点附近,此时精度并没有明显提高,但不会比原来的情况差。这必然是K(ξ1,ξ2)式中的分母绝对值太小,也就是说,是处在,f"""(x)过零或近于零的区域。
对于较光滑的函数,原三点二次插值法的截断误差大致正比于其三阶导数,因此三阶导数较大的区域也是精度最差的区域。f"""(x)过零或近于零的区域中,误差本来就远小于其它区域。综上所述,四点二次插值法与之相比,在三阶导数较大的区域,精度大致改进到相当于节点密度提高二倍后的三点二次插值法;在三阶导数近于0的区域,则不会比原来三点二次插值法差。从实用的角度,可以说已经实现了上文所说的效果。
另外,还可以指出,这个算法中的v1、v2都是由数据表中相邻项的差值产生的,绝对值常常较小,故乘法常可以采用低精度乘。这一点在以较低档的微处理器构成的应用系统中是有实际意义的。如下面AVR单片机的程序中,结果是双字节精度,但其中乘法为单字节。
下面将给出以MCS-96单片机汇编语言和AVR单片机汇编语言编写的程序实例。
实例中,取间隔h为2的整数幂。这样,定点形式的自变量只要采用简单的移位,即可以得出整数的k和纯小数的“,作为下列程序的入口参数。在MCS一96单片机的程序中,k和u均取双字节;在AVR单片机的程序例中,k和u均取单字节,但结果为双字节。
这是一个应用程序中用来查几种数据表的子程序。因为这些表都是增函数,故下面设计中认定“[v2%26;#215;u′+v1]必为正”。表中相邻项的差,符合程序注释中的要求(特别是第二个例子vl、v2为单字节),否则程序需要适当调整。
说明:以下y′、yO加、yl和y2即上文中的fxk-1),f(xk),f(xk+1)和f(xk+2)。
MCS一96和AVR单片机汇编语言插值算法程序见本刊网站www.dpj.com.cn。
系数K(ξ1′,ξ2)反映中点xm处四点二次插值的误差,比原来三点二次插值的误差减小的程度。若f"""(x)是常数,则k(ξ1,ξ2)=0,因而R(xm)=0。也就是说,R(z)第三个零点在xm处,达到上文所述的效果。
对于比较光滑的函数,f"""(x)在小区间内不会变化太大,故k(ξ1,ξ2)式中的分子绝对值应较小。若K(ξ1,ξ2)近于0,则R(xm)也近于0,R(x)的零点仍在xm附近,效果与上述接近。可以证明(限于篇幅.证明略),只要f"""(ξ1)与f"""(ξ)之比在O.5~2之间,则第三个零点必然在xk和xk+1之间。
若K(ξ1,)绝对值较大即f"""(ξ2)与f"""(ξ2)之比距1较远),或,f"""(ξ1)与,f…(ξ2)反号,则零点不在中点附近,此时精度并没有明显提高,但不会比原来的情况差。这必然是K(ξ1,ξ2)式中的分母绝对值太小,也就是说,是处在,f"""(x)过零或近于零的区域。
对于较光滑的函数,原三点二次插值法的截断误差大致正比于其三阶导数,因此三阶导数较大的区域也是精度最差的区域。f"""(x)过零或近于零的区域中,误差本来就远小于其它区域。综上所述,四点二次插值法与之相比,在三阶导数较大的区域,精度大致改进到相当于节点密度提高二倍后的三点二次插值法;在三阶导数近于0的区域,则不会比原来三点二次插值法差。从实用的角度,可以说已经实现了上文所说的效果。
另外,还可以指出,这个算法中的v1、v2都是由数据表中相邻项的差值产生的,绝对值常常较小,故乘法常可以采用低精度乘。这一点在以较低档的微处理器构成的应用系统中是有实际意义的。如下面AVR单片机的程序中,结果是双字节精度,但其中乘法为单字节。
下面将给出以MCS-96单片机汇编语言和AVR单片机汇编语言编写的程序实例。
实例中,取间隔h为2的整数幂。这样,定点形式的自变量只要采用简单的移位,即可以得出整数的k和纯小数的“,作为下列程序的入口参数。在MCS一96单片机的程序中,k和u均取双字节;在AVR单片机的程序例中,k和u均取单字节,但结果为双字节。
这是一个应用程序中用来查几种数据表的子程序。因为这些表都是增函数,故下面设计中认定“[v2%26;#215;u′+v1]必为正”。表中相邻项的差,符合程序注释中的要求(特别是第二个例子vl、v2为单字节),否则程序需要适当调整。
说明:以下y′、yO加、yl和y2即上文中的fxk-1),f(xk),f(xk+1)和f(xk+2)。
MCS一96和AVR单片机汇编语言插值算法程序见本刊网站www.dpj.com.cn。
引用地址:四点二次插值的单片机汇编程序实现
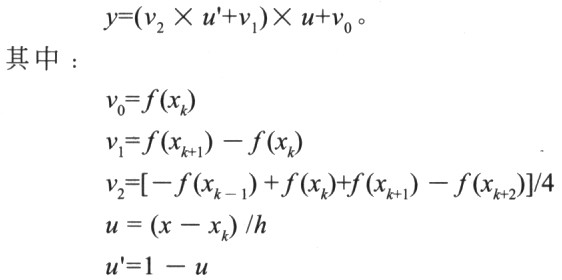 与普通的三点二次插值法对比,可以看出计算量差不多(乘法次数相同,除以4可以用移位实现)。
下面粗略分析其精度。
二次插值误差余项应有三个零点,此法中xk和k+1是其两个零点。显然,如果第三个零点在x1和xk+1的中点处,则其精度和节点密度提高二倍后的三点二次插值法相同。
设(xk-1,xk,xk+1)的三点二次插值误差余项为R1(x),(xk,xk+1xk+2)的三点二次插值误差余项为R2(x)则四点二次插值的误差余项为
与普通的三点二次插值法对比,可以看出计算量差不多(乘法次数相同,除以4可以用移位实现)。
下面粗略分析其精度。
二次插值误差余项应有三个零点,此法中xk和k+1是其两个零点。显然,如果第三个零点在x1和xk+1的中点处,则其精度和节点密度提高二倍后的三点二次插值法相同。
设(xk-1,xk,xk+1)的三点二次插值误差余项为R1(x),(xk,xk+1xk+2)的三点二次插值误差余项为R2(x)则四点二次插值的误差余项为
 系数K(ξ1′,ξ2)反映中点xm处四点二次插值的误差,比原来三点二次插值的误差减小的程度。若f"""(x)是常数,则k(ξ1,ξ2)=0,因而R(xm)=0。也就是说,R(z)第三个零点在xm处,达到上文所述的效果。
对于比较光滑的函数,f"""(x)在小区间内不会变化太大,故k(ξ1,ξ2)式中的分子绝对值应较小。若K(ξ1,ξ2)近于0,则R(xm)也近于0,R(x)的零点仍在xm附近,效果与上述接近。可以证明(限于篇幅.证明略),只要f"""(ξ1)与f"""(ξ)之比在O.5~2之间,则第三个零点必然在xk和xk+1之间。
若K(ξ1,)绝对值较大即f"""(ξ2)与f"""(ξ2)之比距1较远),或,f"""(ξ1)与,f…(ξ2)反号,则零点不在中点附近,此时精度并没有明显提高,但不会比原来的情况差。这必然是K(ξ1,ξ2)式中的分母绝对值太小,也就是说,是处在,f"""(x)过零或近于零的区域。
对于较光滑的函数,原三点二次插值法的截断误差大致正比于其三阶导数,因此三阶导数较大的区域也是精度最差的区域。f"""(x)过零或近于零的区域中,误差本来就远小于其它区域。综上所述,四点二次插值法与之相比,在三阶导数较大的区域,精度大致改进到相当于节点密度提高二倍后的三点二次插值法;在三阶导数近于0的区域,则不会比原来三点二次插值法差。从实用的角度,可以说已经实现了上文所说的效果。
另外,还可以指出,这个算法中的v1、v2都是由数据表中相邻项的差值产生的,绝对值常常较小,故乘法常可以采用低精度乘。这一点在以较低档的微处理器构成的应用系统中是有实际意义的。如下面AVR单片机的程序中,结果是双字节精度,但其中乘法为单字节。
下面将给出以MCS-96单片机汇编语言和AVR单片机汇编语言编写的程序实例。
实例中,取间隔h为2的整数幂。这样,定点形式的自变量只要采用简单的移位,即可以得出整数的k和纯小数的“,作为下列程序的入口参数。在MCS一96单片机的程序中,k和u均取双字节;在AVR单片机的程序例中,k和u均取单字节,但结果为双字节。
这是一个应用程序中用来查几种数据表的子程序。因为这些表都是增函数,故下面设计中认定“[v2%26;#215;u′+v1]必为正”。表中相邻项的差,符合程序注释中的要求(特别是第二个例子vl、v2为单字节),否则程序需要适当调整。
说明:以下y′、yO加、yl和y2即上文中的fxk-1),f(xk),f(xk+1)和f(xk+2)。
MCS一96和AVR单片机汇编语言插值算法程序见本刊网站www.dpj.com.cn。
系数K(ξ1′,ξ2)反映中点xm处四点二次插值的误差,比原来三点二次插值的误差减小的程度。若f"""(x)是常数,则k(ξ1,ξ2)=0,因而R(xm)=0。也就是说,R(z)第三个零点在xm处,达到上文所述的效果。
对于比较光滑的函数,f"""(x)在小区间内不会变化太大,故k(ξ1,ξ2)式中的分子绝对值应较小。若K(ξ1,ξ2)近于0,则R(xm)也近于0,R(x)的零点仍在xm附近,效果与上述接近。可以证明(限于篇幅.证明略),只要f"""(ξ1)与f"""(ξ)之比在O.5~2之间,则第三个零点必然在xk和xk+1之间。
若K(ξ1,)绝对值较大即f"""(ξ2)与f"""(ξ2)之比距1较远),或,f"""(ξ1)与,f…(ξ2)反号,则零点不在中点附近,此时精度并没有明显提高,但不会比原来的情况差。这必然是K(ξ1,ξ2)式中的分母绝对值太小,也就是说,是处在,f"""(x)过零或近于零的区域。
对于较光滑的函数,原三点二次插值法的截断误差大致正比于其三阶导数,因此三阶导数较大的区域也是精度最差的区域。f"""(x)过零或近于零的区域中,误差本来就远小于其它区域。综上所述,四点二次插值法与之相比,在三阶导数较大的区域,精度大致改进到相当于节点密度提高二倍后的三点二次插值法;在三阶导数近于0的区域,则不会比原来三点二次插值法差。从实用的角度,可以说已经实现了上文所说的效果。
另外,还可以指出,这个算法中的v1、v2都是由数据表中相邻项的差值产生的,绝对值常常较小,故乘法常可以采用低精度乘。这一点在以较低档的微处理器构成的应用系统中是有实际意义的。如下面AVR单片机的程序中,结果是双字节精度,但其中乘法为单字节。
下面将给出以MCS-96单片机汇编语言和AVR单片机汇编语言编写的程序实例。
实例中,取间隔h为2的整数幂。这样,定点形式的自变量只要采用简单的移位,即可以得出整数的k和纯小数的“,作为下列程序的入口参数。在MCS一96单片机的程序中,k和u均取双字节;在AVR单片机的程序例中,k和u均取单字节,但结果为双字节。
这是一个应用程序中用来查几种数据表的子程序。因为这些表都是增函数,故下面设计中认定“[v2%26;#215;u′+v1]必为正”。表中相邻项的差,符合程序注释中的要求(特别是第二个例子vl、v2为单字节),否则程序需要适当调整。
说明:以下y′、yO加、yl和y2即上文中的fxk-1),f(xk),f(xk+1)和f(xk+2)。
MCS一96和AVR单片机汇编语言插值算法程序见本刊网站www.dpj.com.cn。
小广播
热门活动
换一批
更多
设计资源 培训 开发板 精华推荐
最新单片机文章
更多精选电路图
更多热门文章
更多每日新闻
更多往期活动
11月24日历史上的今天
厂商技术中心

 嵌入式网络那些事:LwIP协议深度剖析与实战演练
嵌入式网络那些事:LwIP协议深度剖析与实战演练 5962-01-144-7546
5962-01-144-7546












 京公网安备 11010802033920号
京公网安备 11010802033920号