在许多测距系统中,用户端接收到基站发送的帧信号后,便以该帧中特定的位置(称为帧参考时标)为基准发送“回复帧"给基站。基站收到回复帧后,提取它的帧参考时标,并以其作为测距的依据。
通常用户端的系统时钟精度较低(本文提到的系统时钟均指用户端的系统时钟),因此接收到的帧参考时标会存在误差。在用户端经过计算估计出帧参考时标的误差,再用该误差调整发送回复帧的时刻,可实现精确测距。因此测距精度取决于两个因素:帧参考时标误差的估计精度和回复帧发送时刻的调整精度。本文主要讨论如何提高回复帧发送时刻的调整精度。回复帧是由基带码组成的,因此下文中讲的发送时刻的调整均指基带码发送时刻的调整。
发送时刻的调整精度是由发送时刻的调整步长决定的。在一般的数字系统中,发送时刻的调整步长不小于一个系统时钟的周期。本文利用Altera公司的EP20K300EQC240-3型FPGA器件设计了一种成型滤波器组,使发送时刻的调整步长缩短为时钟周期的五分之一,从而将发送时刻的调整精度大幅度地提高。
1 成型滤波器组调整发送时刻的原理
成型滤波器组的设计原理图如图1所示。成型滤波器组包括一

图1 成型滤波器组的设计原理图
2 用FPGA设计成型滤波器
通常,系统时钟频率远高于基带码的速率,因此在成型滤波前,要在基带码的相邻码之间进行内插。内插的方式有多种,通常的内插方法是在发送的基带码的相邻码之间内插“0”。将基带码插“0”后,与低通滤波器的冲激响应卷积,再送到D/A转换器转换成模拟波形就可以实现滤波成型。设计低通滤波器时,为了得到较好的波形,通常采用高阶的FIR滤波器。如果在FPGA中用逻辑单元实现高阶FIR滤波器,会占用大量的逻辑单元。比如在Altera公司的FPGA中用逻辑单元实现一个50阶的FIR滤波器,需要26个乘法器和50个加法器,要占用一千多个逻辑单元。而本文利用FPGA中的ROM,用查表的方法设计同样的FIR滤波器,则只需占用几十个逻辑单元。图2是成型滤波器的设计原理图。该设计包括用数学工具——MATLAB预先设计的部分和在FPGA中实现的部分,MATLAB完成成型滤波后的数据波形文件的设计。FPGA存储设计好的数据波形文件,并用发送的基带码选通相应波形的存储地址,完成滤波成型。
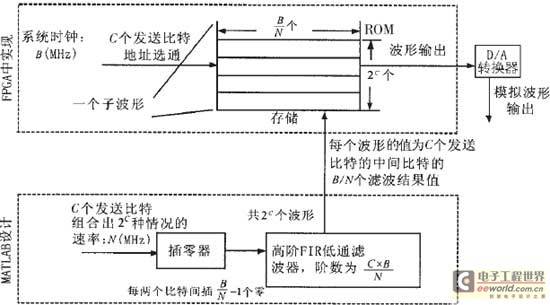
图2 成型滤波器的设计原理图
首先用MATLAB设计数据波形文件。设系统基带码速率为N MHz,系统时钟频率为B MHz。FIR滤波器的阶数为(C为奇数,可根据滤波器的阶数要求进行选择)。FIR滤波器的系数可通过MATLAB进行设计。将C个基带码排列组合成2C种情况。对于每种组合,在C个基带码的相邻码间内插-1个0后,与设计好的滤波器的冲激响应卷积。卷积结果的中间个数据波形值就是该C个基带码组合的中间基带码(简称中间码)的滤波结果值。这个数据波形值可以存储在以该种组合(C个码)为基地址的ROM中。MATLAB可以计算出所有组合下C个基带码的中间码的滤波结果值。
FPGA将所有滤波结果值存入ROM,将每个滤波结果值所对应的基带码组合作为该滤波结果值的存储地址。系统运行时,用一个C位移位寄存器存储C个基带码,作为地址选通ROM,则ROM输出的滤波结果值是C个基带码的中间码的滤波结果值。随着基带码依次到达移位寄存器,移位寄存器中C个基带码的中间码也被后面的基带码依次替换, ROM输出的将是依次到达的中间码的滤波结果值,从而实现基带码的滤波成型。
图2中ROM存储的数据是设计一个成型滤波器得到的波形数据,为了与下面成型滤波器组的存储数据相区别,将图2中ROM存储的所有波形数据统称为一个子波形。
3 在FPGA中用成型滤波器组调整发送时刻的方法
图3是成型滤波器组的实现方案图。图中的FPGA的ROM中存储了E个子波形,称为一个成型滤波器组。第一个子波形就是图2所设计的子波形,称为原来的子波形。之后的E-1个子波形是原来的子波形以时钟周期的1/E循环左移1,2,...,E-1次得到的。如何得到这些移位后的子波形是设计的关键。由于波形的移位在MATLAB中是以数值的变化体现出来的,而通过MATLAB计算可以得到数值精度很高的波形数据,所以用MATLAB设计的波形,移位可以远小于时钟周期,因此可以很容易用MATLAB得到以时钟周期的1/E循环左移后的各个子波形。

图3 成型滤波器组的实现方案图
各移位后的子波形按循环左移大小依次存储在ROM中。因此一个时钟周期的延时被划分成了E个区间,将测距误差除以时钟周期,得到余数R,计算出R落在了E个区间中的哪个。选择该区间的子波形,将该子波形送到D/A转换器转换成模拟波形后再输出,就可将发送时刻的调整步长降到时钟周期的1/E。实际设计时,在MATLAB中将FIR滤波器的冲激响应以时钟周期的1/E循环左移,再与插零后的基带码卷积,就实现了子波形的循环左移。而通常的系统实时产生的波形是由系统时钟控制的,延时不会小于一个时钟周期,因此其调整精度远不如用MATLAB设计的成型滤波器组的方法。[page]
上面介绍的是子波形循环左移的方法,也可以将子波形循环右移,道理是一样的。
4 实例与仿真
4.1 子波形的设计与仿真
本设计所应用的测距系统的基带码速率为2MHz,系统时钟频率为20MHz,因此在2MHz基带码的相邻比特间内插个“0”,然后通过阶(C选为5)的FIR滤波器就可实现成型滤波。5个基带码可排列成32种组合,图4是其中的一种基
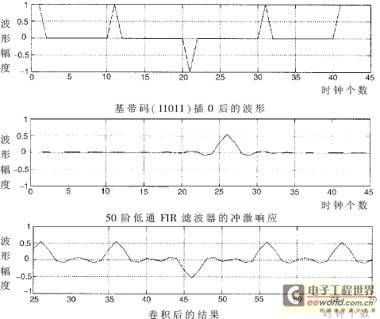
图4 基带码组合11011的成型滤波的仿真结果
4.2 成型滤波器组的设计
由于时钟周期为50ns,当要求最小调整步长不大于10ns时,在MATLAB中将FIR滤波器的冲激响应以时钟周期的1/5循环左移,再与插零后的基带码进行卷积,就可以得到以时钟周期的1/5循环左移0,1,2,3,4次后形成的五个子波形。图5是组合为11011的基带码经上述方式产生的五个子波形的图。

图5组合为11011的基带码经上述方式产生的五个子波形的图
从图5中中央的两条虚线可以看出,经五次移位后的第五个子波形的0码与原来的子波形的0码相比,延时为4/5个时钟周期。这样就将调整发送时刻的步长减小到时钟周期的1/5,大幅度提高了测距精度。
假设估计出的测距误差是72ns,如果不采用成型滤波器的方法,调整步长为50ns,调整一个时钟后,会产生72-50=22ns的调整精度误差。而采用成型滤波器后,调整的步长缩小为10ns,在发送时将第三个数据波形送到D/A转换器转换成模拟波形,再将模拟波形送出就可使调整精度的误差降低到72-50-2×10=2ns。图6是采用成型滤波器组前后调整精度的误差对比图(假设测距误差估计服从高斯分布,均值为25ns,标准差为25ns)。
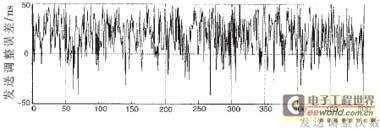
(a) 采用成形滤波器组前的发送调整误差
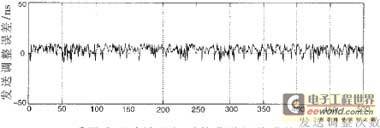
(b) 采用成形滤波器组后的发送调整误差
图6 采用成型滤波器组前后调整精度的误差对比图
经图中的数据计算得出:在不采用成型滤波器组的情况下,发送调整误差的标准差为18.17ns。采用成型滤波器组后,发送调整误差的标准差为4.42ns,是不采用成型滤波器组时的。
成型滤波器组占用ROM的数量是由发送时刻调整的精度、成型滤波器的阶数、波形数值量化的比特数、每个基带码的时钟采样点个数等因素决定的。对上面的例子而言,每五个基带码组合要生成10个8比特的波形数据,因此所存储的地址长度为4比特,存储单位是字节。五个基带码共有32种组合,所以一个子波形的地址长度为4+5=9位。在调整步长是时钟的1/5的要求下,要另加3比特基地址来存储五个子波形。所以整个成型滤波器组总共消耗的ROM的数量为2(4+5+3)×8=32768比特。
除采用数字电路方式外,许多系统还用模拟电路的方式调整发送时刻:将基带码通过模拟触发电路发送,而测距误差通过模拟触发电路控制基带码的发送时刻。这种方式在理论上调整发送时刻的步长更小,但与数字电路相比,易受到温度、噪声等多种因素的影响,可靠性差得多。而本文提出的方法是用数字的方式实现的,稳定性和可靠性均有无可比拟的优越性。
本文设计的成型滤波器充分地利用了硬件中所剩的ROM资源,占用了很少的逻辑单元。用该成型滤波器构成的成型滤波器组,可将基带码发送时刻的调整步长减小到时钟周期的几分之一,甚至十几分之一,因此大幅度提高了发送时刻的调整精度。本文的设计已被应用于某个测距系统中,取得了很好的效果。该设计还可应用于其它许多测距系统中,如定位系统、二次雷达等,因此有较高的实用价值。
参考文献
1仵国锋,程 博, 胡捍英. 一种高速FIR成型滤波器的设计和实现. 无线通信技术,2001(2)
2 Elliott D. Kaplan著, 邱致和,王万义译.GPS原理与应用.北京:电子工业出版社,2002
上一篇:系统互通性的模型与测量研究
下一篇:电感智能数字化测量
推荐阅读最新更新时间:2024-03-30 22:47








 高频电路设计与制作 (市川裕一,青木胜,卓圣鹏 著)
高频电路设计与制作 (市川裕一,青木胜,卓圣鹏 著) 控制系统计算机辅助设计 — MATLAB语言与应用
控制系统计算机辅助设计 — MATLAB语言与应用









 京公网安备 11010802033920号
京公网安备 11010802033920号