1 引言
缺陷接地结构(Defected Ground Structure,DGS)是微波领域新近发展的热点之一,它由光子带隙结构(PBG)发展而来。DGS通过在接地板上刻蚀缺陷图案,改变接地板上屏蔽电流的分布,从而间接改变传输线的等效电感和等效电容,获得慢波特性和禁带特性。慢波特性可以让微波传输线结构更加紧凑,而禁带特性可以抑制谐波杂波等无用信号。该技术现已被应用于滤波器设计中,可使滤波器抑制谐波的能力更为突出。
本文中提出了一种正六边形的地面缺陷结构作为DGS基本单元。设计的这个DGS单元结构,其单元等效电路可由RLC并联谐振单元表示,通过改变地面缺陷单元的正六边形的面积和狭槽的宽度,可以很容易控制等效电感和电容。从而调整其频率响应特性。本文通过对六边形尺寸参数变化的研究,提出了对应的低通滤波器的等效电路,设计了一个基于五个正六边形DGS的滤波器,在ADS中对等效电路的仿真结果与HFSS中的仿真结果很吻合。
2 正六边形DGS低通滤波器
2.1 DGS及其等效电路
正六边形DGS单元结构如图1(a)所示。在微带线的下方接地板上蚀刻出2个对称的正六边形并由一狭槽连接。本文采用介电常数为3.2,厚度为0.787mm的基板。其50Ω微带线长度d为1.88 mm,微带线两旁蚀刻区域形成的等效电感L和中间的狭槽形成的等效电容C组成LC并联的谐振电路的频率响应在特定频点上产生极点。其有耗等效电路是一个并联谐振RLC电路。如图1(b)所示,该RLC电路由一个等效并联电容C,一个并联电感L 以及电阻R 构成。这些参数可以通过对该结构进行EM仿真及以下公式提取出来
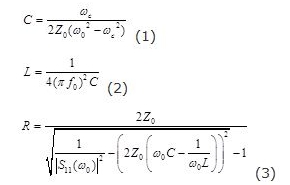
式中ω0是谐振角频率;ωc代表3 dB截止角频率;Z0指传输线的特征阻抗,这里Z0为50 Ω。
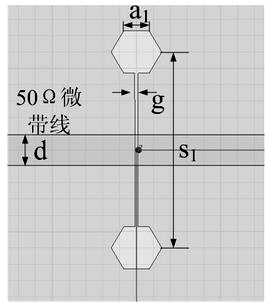
图1(a)正六边形的DGS单元
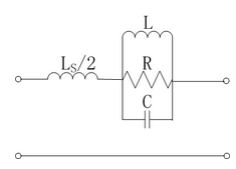
图1(b)等效电路
对图1(a)的六边形DGS单元在HFSS中建模进行EM仿真,观察其谐振频率随着六边形的边长的变化情况。其中,蚀刻狭槽的长度为s=12 mm,宽度g= 0.2 mm保持不变,而六边形的边长从1.0 mm到2.5 mm变化,从仿真的结果可以看出,由于DGS图形的中间狭槽长度宽度不变,等效电容基本不变,而其等效电感随正六边形的面积增大而增加[5]。由可得3 dB截止频率降低,LC谐振电路的谐振频率也相应的从6.32 GHz降低为4.43 GHz,如图2所示。
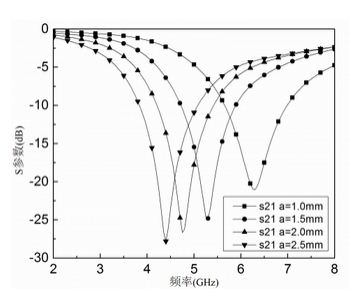
图2 正六边形边长对谐振频率的影响[page]
2.2 低通滤波器设计
如上面的分析可以看出,正六边形DGS结构可以用来设计低通滤波器或抑止其寄生的旁带。但是该结构也存在一些缺陷,如在高频范围内没有足够的抑止,且存在着截止特性缓慢的情况。因此,在单个DGS单元上加上一个H形的并联枝节来增加微带线和正六边形DGS单元之间的耦合电容。这样不仅可以最大限度地减小LPF的尺寸,而且能够提高LPF的阻带特性。图3(a)是带H形并联支节的DGS单元,(b)是其等效电路。
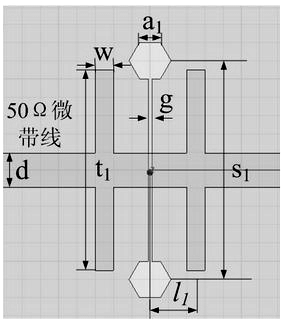
图3(a)H形支节的DGS单元
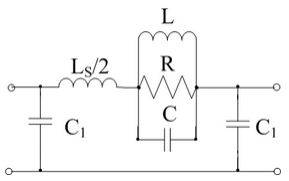
图3(b)等效电路
其中,l1 = 2.5 mm,w = 1 mm,a1 = 1.2 mm,d = 1.88 mm。在其它尺寸不变的情况下,并联枝节的长度t1从4 mm到10 mm逐渐增加,由仿真结果可以看出,随着l的增加,等效电路的电容也随之增加,从而带外的抑止也随着提高。而在2.41 GHz的3 dB截止频率并没有平移,只是衰减变得更深。并联支节的长度t1为10 mm时相对于4 mm的带外抑止提高了差不多10 dB,如图4所示。
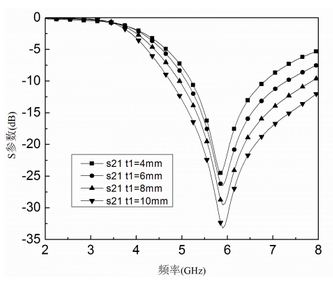
图4 H型开槽长度对谐振频率的影响
为了获得性能良好的频率响应特性,并提高其带外抑止,必须增加正六边形DGS单元的数目,在这里设计的低通滤波器采用五个正六边形DGS单元。其对称结构如图5(a)所示,对应的等效电路如图5(b)所示。
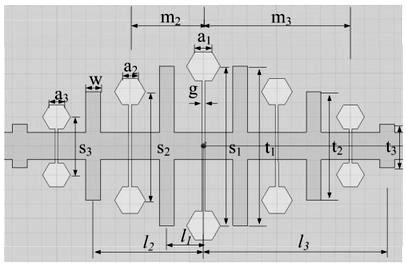
图5 (a)具有五个DGS单元的LPF
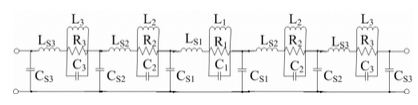
图5 (b)等效电路
除了t3之外,其它的参数都通过对单个单元进行分析而得到。它们的尺寸分别为:w = 1 mm,g = 0.2 mm,a1 = 1.15 mm,a2 = 1.05 mm,a3 = 0.95 mm,s1 = 11 mm,s2 = 7.5 mm,s3 = 4 mm,l1 = 2.5 mm,l2 = 7.5 mm,l3 = 12.5 mm,m2 = 5.1 mm,m3 = 10.1 mm,t1 = 11 mm,t2 = 7.5 mm。
图6是采用五个DGS单元的低通滤波器随着并联支节长度t3的变化的仿真结果。由于并联支节长度增加使得图5(b)所示的等效电容CS3也随着增加。这样使得带外抑止也随之增加,而且通带到带阻的衰减也变得更加陡峭。同时我们也注意到,其带内特性如插入损耗和回波损耗却都有所增加。因此在设计的过程之中必须兼顾通带和阻带这两方面的特性。[page]
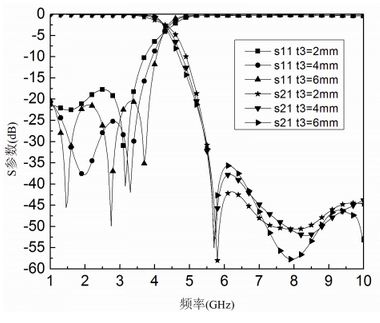
图6 LPF频率响应随t3从2mm到6mm变化的仿真结果的比较
通过EM仿真和等效电路的仿真可以得到优化后的低通滤波器特性,当t3= 3 mm时,其仿真结果如图7所示。
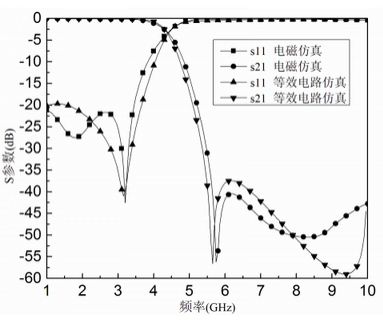
图7 LPF的电磁仿真与等效电路仿真结果比较
对应的其等效网络的参数为:C1 = 0.627 pF,C2 = 0.109 pF,C3 = 0.067 pF,L1 = 1.25 nH,L2 = 1.608 nH,L3 = 0.515 nH,R1 = 8.87 kΩ,R2 = 2.39 kΩ,R3 = 1.15 kΩ,CS1 = 1.238 pF,CS2 = 0.927 pF,CS3 = 0.303 pF,LS1 = 1.01 nH,LS2 = 0.802 nH,LS3 = 1.128 nH。
为了验证这个等效电路的正确性,通过ADS对其等效电路进行了仿真。从仿真结果比较可以看出,两者吻合较好。对于低通滤波器的频率特性,对应的3 dB截止频率为4.42 GHz,在通带范围内其S11低于-21 dB.而在阻带,从5.5 GHz到10 GHz这个很宽的频带范围内可以得到低于-40 dB的带外抑止。使用H形并联枝节的DGS结构与普通的DGS结构相比在阻带内能获得更高的衰减和谐波抑止,同时实现陡峭的下降特性。
3 结论
文章提出了一种基于正六边形的DGS单元的低通滤波器,并且通过加入H形的并联枝节来增加它的等效电容从而提高它的带外抑止。提出了该DGS低通滤波器的等效电路模型。通过对DGS单元的尺寸参数分析得到该低通滤波器的等效电路元件值。设计了一个基于五个正六边形DGS单元的低通滤波器。在HFSS中对其建模仿真的结果跟在ADS中对其等效电路进行仿真的结果进行比较基本一致。截止频率响应非常的陡峭,能够获得低于-21 dB的S11,3 dB的截止频率为4.42 GHz。且在5.5 GHz到10 GHz的宽频带范围内得到低于-40 dB的阻带抑止。
关键字:低通滤波器 RLC 等效电路
引用地址:基于正六边形DGS单元的微带低通滤波器设计
缺陷接地结构(Defected Ground Structure,DGS)是微波领域新近发展的热点之一,它由光子带隙结构(PBG)发展而来。DGS通过在接地板上刻蚀缺陷图案,改变接地板上屏蔽电流的分布,从而间接改变传输线的等效电感和等效电容,获得慢波特性和禁带特性。慢波特性可以让微波传输线结构更加紧凑,而禁带特性可以抑制谐波杂波等无用信号。该技术现已被应用于滤波器设计中,可使滤波器抑制谐波的能力更为突出。
本文中提出了一种正六边形的地面缺陷结构作为DGS基本单元。设计的这个DGS单元结构,其单元等效电路可由RLC并联谐振单元表示,通过改变地面缺陷单元的正六边形的面积和狭槽的宽度,可以很容易控制等效电感和电容。从而调整其频率响应特性。本文通过对六边形尺寸参数变化的研究,提出了对应的低通滤波器的等效电路,设计了一个基于五个正六边形DGS的滤波器,在ADS中对等效电路的仿真结果与HFSS中的仿真结果很吻合。
2 正六边形DGS低通滤波器
2.1 DGS及其等效电路
正六边形DGS单元结构如图1(a)所示。在微带线的下方接地板上蚀刻出2个对称的正六边形并由一狭槽连接。本文采用介电常数为3.2,厚度为0.787mm的基板。其50Ω微带线长度d为1.88 mm,微带线两旁蚀刻区域形成的等效电感L和中间的狭槽形成的等效电容C组成LC并联的谐振电路的频率响应在特定频点上产生极点。其有耗等效电路是一个并联谐振RLC电路。如图1(b)所示,该RLC电路由一个等效并联电容C,一个并联电感L 以及电阻R 构成。这些参数可以通过对该结构进行EM仿真及以下公式提取出来
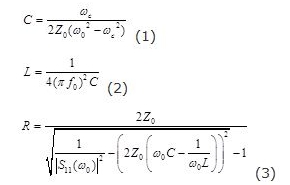
式中ω0是谐振角频率;ωc代表3 dB截止角频率;Z0指传输线的特征阻抗,这里Z0为50 Ω。

图1(a)正六边形的DGS单元

图1(b)等效电路
对图1(a)的六边形DGS单元在HFSS中建模进行EM仿真,观察其谐振频率随着六边形的边长的变化情况。其中,蚀刻狭槽的长度为s=12 mm,宽度g= 0.2 mm保持不变,而六边形的边长从1.0 mm到2.5 mm变化,从仿真的结果可以看出,由于DGS图形的中间狭槽长度宽度不变,等效电容基本不变,而其等效电感随正六边形的面积增大而增加[5]。由可得3 dB截止频率降低,LC谐振电路的谐振频率也相应的从6.32 GHz降低为4.43 GHz,如图2所示。

图2 正六边形边长对谐振频率的影响[page]
2.2 低通滤波器设计
如上面的分析可以看出,正六边形DGS结构可以用来设计低通滤波器或抑止其寄生的旁带。但是该结构也存在一些缺陷,如在高频范围内没有足够的抑止,且存在着截止特性缓慢的情况。因此,在单个DGS单元上加上一个H形的并联枝节来增加微带线和正六边形DGS单元之间的耦合电容。这样不仅可以最大限度地减小LPF的尺寸,而且能够提高LPF的阻带特性。图3(a)是带H形并联支节的DGS单元,(b)是其等效电路。

图3(a)H形支节的DGS单元

图3(b)等效电路
其中,l1 = 2.5 mm,w = 1 mm,a1 = 1.2 mm,d = 1.88 mm。在其它尺寸不变的情况下,并联枝节的长度t1从4 mm到10 mm逐渐增加,由仿真结果可以看出,随着l的增加,等效电路的电容也随之增加,从而带外的抑止也随着提高。而在2.41 GHz的3 dB截止频率并没有平移,只是衰减变得更深。并联支节的长度t1为10 mm时相对于4 mm的带外抑止提高了差不多10 dB,如图4所示。

图4 H型开槽长度对谐振频率的影响
为了获得性能良好的频率响应特性,并提高其带外抑止,必须增加正六边形DGS单元的数目,在这里设计的低通滤波器采用五个正六边形DGS单元。其对称结构如图5(a)所示,对应的等效电路如图5(b)所示。

图5 (a)具有五个DGS单元的LPF

图5 (b)等效电路
除了t3之外,其它的参数都通过对单个单元进行分析而得到。它们的尺寸分别为:w = 1 mm,g = 0.2 mm,a1 = 1.15 mm,a2 = 1.05 mm,a3 = 0.95 mm,s1 = 11 mm,s2 = 7.5 mm,s3 = 4 mm,l1 = 2.5 mm,l2 = 7.5 mm,l3 = 12.5 mm,m2 = 5.1 mm,m3 = 10.1 mm,t1 = 11 mm,t2 = 7.5 mm。
图6是采用五个DGS单元的低通滤波器随着并联支节长度t3的变化的仿真结果。由于并联支节长度增加使得图5(b)所示的等效电容CS3也随着增加。这样使得带外抑止也随之增加,而且通带到带阻的衰减也变得更加陡峭。同时我们也注意到,其带内特性如插入损耗和回波损耗却都有所增加。因此在设计的过程之中必须兼顾通带和阻带这两方面的特性。[page]

图6 LPF频率响应随t3从2mm到6mm变化的仿真结果的比较
通过EM仿真和等效电路的仿真可以得到优化后的低通滤波器特性,当t3= 3 mm时,其仿真结果如图7所示。

图7 LPF的电磁仿真与等效电路仿真结果比较
对应的其等效网络的参数为:C1 = 0.627 pF,C2 = 0.109 pF,C3 = 0.067 pF,L1 = 1.25 nH,L2 = 1.608 nH,L3 = 0.515 nH,R1 = 8.87 kΩ,R2 = 2.39 kΩ,R3 = 1.15 kΩ,CS1 = 1.238 pF,CS2 = 0.927 pF,CS3 = 0.303 pF,LS1 = 1.01 nH,LS2 = 0.802 nH,LS3 = 1.128 nH。
为了验证这个等效电路的正确性,通过ADS对其等效电路进行了仿真。从仿真结果比较可以看出,两者吻合较好。对于低通滤波器的频率特性,对应的3 dB截止频率为4.42 GHz,在通带范围内其S11低于-21 dB.而在阻带,从5.5 GHz到10 GHz这个很宽的频带范围内可以得到低于-40 dB的带外抑止。使用H形并联枝节的DGS结构与普通的DGS结构相比在阻带内能获得更高的衰减和谐波抑止,同时实现陡峭的下降特性。
3 结论
文章提出了一种基于正六边形的DGS单元的低通滤波器,并且通过加入H形的并联枝节来增加它的等效电容从而提高它的带外抑止。提出了该DGS低通滤波器的等效电路模型。通过对DGS单元的尺寸参数分析得到该低通滤波器的等效电路元件值。设计了一个基于五个正六边形DGS单元的低通滤波器。在HFSS中对其建模仿真的结果跟在ADS中对其等效电路进行仿真的结果进行比较基本一致。截止频率响应非常的陡峭,能够获得低于-21 dB的S11,3 dB的截止频率为4.42 GHz。且在5.5 GHz到10 GHz的宽频带范围内得到低于-40 dB的阻带抑止。
上一篇:用示波器执行pass/fail测试
下一篇:在S参数级联过程中防止假信号的方法
推荐阅读最新更新时间:2024-03-30 22:53
基于数字鉴相的自由轴法RLC测量

0 引 言 R,L,C是电子电路及系统的主要元件,R,L,C参数的测量方法有电桥法、谐振法、伏安法。其中,电桥法具有较高的测量精度,但电路复杂且需要进行电桥平衡调节,不宜完成快速的自动测量。由于测量方法的制约,谐振法需要很高的频率激励信号,一般无法完成较高精度的测量。伏安法在设计中必须完成矢量测量及除法运算,为了实现高精度测量,还需要采用低失真的正弦波信号和高精度的A/D,早期实现比较困难。由于计算机技术的发展,智能仪器的计算能力和控制能力有了较大提高,使伏安法在实际中得到广泛应用。 伏安法测量中,有固定轴法和自由轴法两种,固定轴法要求相敏检波器的相位参考基准严格地与标准阻抗电压的相位相同,对硬件要求很高,并且存在同相误差
[测试测量]

基于微控制器的自由轴法RLC测量方法研究

0 引 言 R,L,C是电子电路及系统的主要元件,R,L,C参数的测量方法有电桥法、谐振法、伏安法。其中,电桥法具有较高的测量精度,但电路复杂且需要进行电桥平衡调节,不宜完成快速的自动测量。由于测量方法的制约,谐振法需要很高的频率激励信号,一般无法完成较高精度的测量。伏安法在设计中必须完成矢量测量及除法运算,为了实现高精度测量,还需要采用低失真的正弦波信号和高精度的A/D,早期实现比较困难。由于计算机技术的发展,智能仪器的计算能力和控制能力有了较大提高,使伏安法在实际中得到广泛应用。 伏安法测量中,有固定轴法和自由轴法两种,固定轴法要求相敏检波器的相位参考基准严格地与标准阻抗电压的相位相同,对硬件要求很高,并且存在同相误差,已很少
[单片机]

瞬时无功功率理论谐波检测中低通滤波器的应用

0 引言 随着电力电子技术的发展,电力电子装置带来的谐波问题对电网安全、稳定、经济运行带来了极大影响,人们急需能够在电网中对所有谐波参数进行实时准确的检测与分析。电网谐波由于受非线性、随机性、分布性、非平稳性及复杂性等因素影响,对谐波进行准确实时检测非常重要且并非易事,目前人们正在不断探索更为有效的谐波实时检测方法及其实现技术。 目前,电网谐波检测主要通过谐波电流的检测来实现。谐波检测主要有以下几种方法:(1)采用模拟带通或带阻滤波器检测,(2)基于广义瞬时无功功率的谐波检测法,和瞬时无功功率理论一样,在解决谐波总量实时检测方面很有优势,在谐波实时监测领域有着广泛应用,本文主要是引用该方法进行谐波实时检测。(3)基于傅立叶变
[测试测量]

什么是低通滤波器

低通滤波器是指车载功放中能够让低频信号通过而不让中、高频信号通过的电路,其作用是滤去音频信号中的中音和高音成分,增强低音成分以驱动扬声器的低音单元。由于车载功放大部分都是全频段功放,通常采用AB类放大设计,功率损耗比较大,所以滤除低频段的信号,只推动中高频扬声器是节省功率、保证音质的最佳选择。此外高通滤波器常常和低通滤波器成对出现,不论哪一种,都是为了把一定的声音频率送到应该去的单元。 高通与低通滤波器的最常见拓扑是Sallen Key,它只需一个运放(图1a和1b)。多通(道)滤波器常用作带通滤波器(图1c),而且它还只需要一个运放。图2及图3示出了双二阶滤波器部分的拓扑。每种结构都能实现完整的通用滤波器传递函数。图2所示电路
[模拟电子]

CMOS运算放大器LMC6062/6082及其应用

摘要:LMC6062/6082是一种高精度、高输入阻抗的CMOS型运算放大器,文中介绍了它的特点、电气特性及使用中的一些技术问题,并给出了它的三个应用实例。 关键词:CMOS运算放大器;LMC6062/6082;特点 1. LMC6062/6082的特点 LMC6062/6082是国家半导体公司生产的双CMOS运算放大器。以往的CMOS运算放大器由于输入偏置电压较高,不适合用于要求高精度的场合。然而LMC6062/6082的优良性能使它能与高精度的双极型运放相匹敌,从而大大地拓宽了CMOS运放的应用范围。 LMC6062/6082最大额定电压为16V,可在5~15V单电源下工作。也可在正、负电源供
[模拟电子]


 高频电路设计与制作 (市川裕一,青木胜,卓圣鹏 著)
高频电路设计与制作 (市川裕一,青木胜,卓圣鹏 著) 控制系统计算机辅助设计 — MATLAB语言与应用
控制系统计算机辅助设计 — MATLAB语言与应用









 京公网安备 11010802033920号
京公网安备 11010802033920号