摘要:讨论了比率测量方法的优点,介绍了运用感应耦合比率臂和差动式电容位移传感器设计的高精度微小位移测量系统。给出了一种实验系统的设计例子和主要的测试结果,说明了该设计在小位移测量中的有效性。
关键词:位移测量 感应耦合比率臂 电容传感器 纳米测量
各种物理量(如温度、压力、位移、振动、速度、流量与扭矩)或者是浓度、酸碱度等化学量,一般都需要用适当的传感器将其转换为电学量后才便于检测和控制。常用的电气测量方法有很多种,依据测量误差与测量方法相关联的特点,可以将现有的各种测量方法分为如下三大类:
(1)直接测量法:直接测量未知量的数据;
(2)差值测量法:测量未知量与已知量之差,间接获得被测量的值;
(3)比率测量法:测量未知量与已知量之比值,间接获得被测量的值。
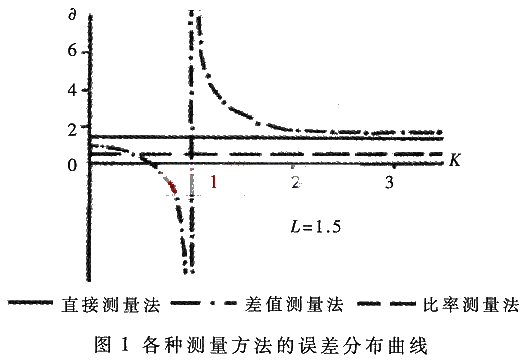
测量的过程就是要在未知量和已知量间建立起一定的关系,最后获得被测量的大小。在采用上述不同的测量方法的,测量装置和过程引入的误差是不一样的。如在直接测量法中,因为测量时间与环境的变化会引入一个系统误差;而采用差值测量法时,由于两个被比较的元件的外界条件相同,检测它们的差值可在很大程度上消除上述系统误差,尤其是利用零偏法时,差值测量可以获得相当精确的结果,不过所测得的两个量之差值仍随着外部条件的变动而变化。采用比率测量法能够显著减小在一级近似下被测量中依赖于外界条件以乘积因子形式出现的误差项,从而具有优于差值测量法的抗干扰性能。
 1 比率测量法
一个物理量f,其值取决于外界因素如t(温度)、u(电压)……等,其一阶展开式为:
f=f0+(аf/аt)0Δt+(аf/аu)0Δu+A (1)
为简化数字运算,只考虑存在一个干扰因素的情况,参考量f1与被测量f2可以分别写作:f1=f01(1+β1Δt)和f2=f02(1+β2Δt),此处β1=1/(f01)(аf1)/(аt)0, β2=1/(f02)[(аf2)/(аt)]0,且有β1Δt<<1,β2Δt<<1。容易求出上述三种方法中的相对测量误差各为:
а绝对=β2Δt=Lβ1ΔT (2)
а差值=[(f02β2-f01β1)Δt/(f02-f01)]=[(LK-1)/(K-1)]β1ΔT (3)
а比率=(β2-β1) Δt=(L-1)β1Δt (4)
1 比率测量法
一个物理量f,其值取决于外界因素如t(温度)、u(电压)……等,其一阶展开式为:
f=f0+(аf/аt)0Δt+(аf/аu)0Δu+A (1)
为简化数字运算,只考虑存在一个干扰因素的情况,参考量f1与被测量f2可以分别写作:f1=f01(1+β1Δt)和f2=f02(1+β2Δt),此处β1=1/(f01)(аf1)/(аt)0, β2=1/(f02)[(аf2)/(аt)]0,且有β1Δt<<1,β2Δt<<1。容易求出上述三种方法中的相对测量误差各为:
а绝对=β2Δt=Lβ1ΔT (2)
а差值=[(f02β2-f01β1)Δt/(f02-f01)]=[(LK-1)/(K-1)]β1ΔT (3)
а比率=(β2-β1) Δt=(L-1)β1Δt (4)
 其中L=(β2)/(β1),K=(f02)/(f01)。图1表示取L=1.5时相对误差随元件值的分布情况。可以看出,比率测量法在很宽的测量范围内均具有良好的抗干扰能力。当存在多个影响因素或者在分析由上述方法组合成的测量装置时,可根据叠加原理按系统误差的理论综合评定其精度。
2 电容位移传感器与比率测量
电容式微小位测量系统是近年来发展最快的位移测量技术之一。众所周知,用两块平行的金属板就可以构成一个电容位移传感器,其电容量由极板的相对有效面积、极板间距以及填充的介质特性所决定。只要被测特体位置的移动改变了电容器上述任何一个结构参数,传感器的电容量就会发生变化,通过测量电容量的变动即可精确地知道特体位移的大小。
其中L=(β2)/(β1),K=(f02)/(f01)。图1表示取L=1.5时相对误差随元件值的分布情况。可以看出,比率测量法在很宽的测量范围内均具有良好的抗干扰能力。当存在多个影响因素或者在分析由上述方法组合成的测量装置时,可根据叠加原理按系统误差的理论综合评定其精度。
2 电容位移传感器与比率测量
电容式微小位测量系统是近年来发展最快的位移测量技术之一。众所周知,用两块平行的金属板就可以构成一个电容位移传感器,其电容量由极板的相对有效面积、极板间距以及填充的介质特性所决定。只要被测特体位置的移动改变了电容器上述任何一个结构参数,传感器的电容量就会发生变化,通过测量电容量的变动即可精确地知道特体位移的大小。
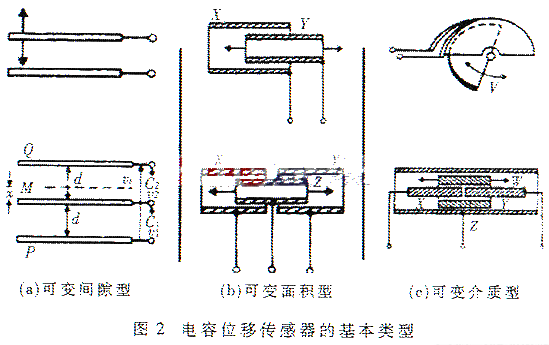
 电容位移传感器的三种基本类型如图2所示。其具体结构可视实际运用的场合灵活多变,电容极板可以是平面的或者球面的;运行电极可以采用水银等导电液体。图2所示的三种基本类型均可组成差动式结构,如各分类中下部图形所示。采用差动式结构能够提高传感器线路的输出灵敏度,减小非线性,还能在一定程序上抑制由静电吸引带来的误差。当要求测量系统具有很高的分辨力时,一般是保持极板面积相对固定而使电容传感器极板间隙随被测位移改变,即如图2(a)所示的结构。反之,采用保持间隔恒定而让极板相对面积可变的结构,则可以在相当大的动态范围内获得线性的响应。
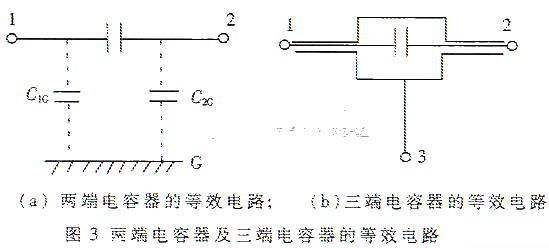
一般情况下,电阻、电感和电容等电子元件均被盾作双端元件。两端电容器的等效电路示如图3(a)。由于各端钮对附近导电物体的分布电容C1G、C2G是变化的,所以其总电容C12+[(C1G%26;#215;C2G)/(C1G+C2G)也是不稳定的。如果电容式传位移传感设计成这种简单的结构,外界干扰会很大。为了消除上述分布参数的影响,必须对电容传感器进行完善的静电屏蔽,形成如图3(b)的结构,称之为三端电容器。这样的三端电容元件中,由极板形成的直接电容C12是确定的,但是C13、C23仍受引线芯屏间电容的影响。如何排队三端电容中分布参数的影响?怎样准确测量与位移相关的直接电容的大小呢?
电容位移传感器的三种基本类型如图2所示。其具体结构可视实际运用的场合灵活多变,电容极板可以是平面的或者球面的;运行电极可以采用水银等导电液体。图2所示的三种基本类型均可组成差动式结构,如各分类中下部图形所示。采用差动式结构能够提高传感器线路的输出灵敏度,减小非线性,还能在一定程序上抑制由静电吸引带来的误差。当要求测量系统具有很高的分辨力时,一般是保持极板面积相对固定而使电容传感器极板间隙随被测位移改变,即如图2(a)所示的结构。反之,采用保持间隔恒定而让极板相对面积可变的结构,则可以在相当大的动态范围内获得线性的响应。
一般情况下,电阻、电感和电容等电子元件均被盾作双端元件。两端电容器的等效电路示如图3(a)。由于各端钮对附近导电物体的分布电容C1G、C2G是变化的,所以其总电容C12+[(C1G%26;#215;C2G)/(C1G+C2G)也是不稳定的。如果电容式传位移传感设计成这种简单的结构,外界干扰会很大。为了消除上述分布参数的影响,必须对电容传感器进行完善的静电屏蔽,形成如图3(b)的结构,称之为三端电容器。这样的三端电容元件中,由极板形成的直接电容C12是确定的,但是C13、C23仍受引线芯屏间电容的影响。如何排队三端电容中分布参数的影响?怎样准确测量与位移相关的直接电容的大小呢?
 上世纪五十年代在电力工学和计算学领域出现了一种新型的电压比率器件——感应耦合比率臂,它的突出特点是分压精度高,可达10 -8量级以上;输出阻抗低,能做到10mΩ以下;长期稳定性非常好,年漂移率保持在10 -9的水平。其后,感应分压器的理论与工艺日臻完善,极大地提高了电工测量和标准计量的精度,实现了对小电容的高精度测量,进而以计算电容与感应分压器为基准导出了电阻、电感等的计量标准。这一成就也对精密测量领域产生了积极的推动作用。
如果将两个三端电容串接起来,分别用两个信号源供电,就形成了如图4所示的等效电路,其中,Y12=jωC12,Y’12=jωC"12。在公共点D与接地端之间连接一个检流计,调节两个外加电压的幅值和相位,使通过两个直接电容流向D点的电流大小相等、方向相反,直道检流计指零,便可得到下面的关系式:
C12/C’12=-(U2/U1) (5)
可见,只要知道了两个电压之比也就知道了两个三端电容的直接电容之比,于是就可以准确测量传感器相应的位移。两个电压源如果用感应耦合比率臂来实现,端钮对屏蔽的导纳对测量结果将没有明显的影响,因为Y23、Y’23在电路不平衡时只影响灵敏度,而当线路达到平衡状态时就没有影响了。至于Y13、Y’13引起的分压误差,则可以得到极大的降低,只要信号源的内阻足够小即可。如前所述,感应耦合比较率臂正好具有这一优良特性。
上世纪五十年代在电力工学和计算学领域出现了一种新型的电压比率器件——感应耦合比率臂,它的突出特点是分压精度高,可达10 -8量级以上;输出阻抗低,能做到10mΩ以下;长期稳定性非常好,年漂移率保持在10 -9的水平。其后,感应分压器的理论与工艺日臻完善,极大地提高了电工测量和标准计量的精度,实现了对小电容的高精度测量,进而以计算电容与感应分压器为基准导出了电阻、电感等的计量标准。这一成就也对精密测量领域产生了积极的推动作用。
如果将两个三端电容串接起来,分别用两个信号源供电,就形成了如图4所示的等效电路,其中,Y12=jωC12,Y’12=jωC"12。在公共点D与接地端之间连接一个检流计,调节两个外加电压的幅值和相位,使通过两个直接电容流向D点的电流大小相等、方向相反,直道检流计指零,便可得到下面的关系式:
C12/C’12=-(U2/U1) (5)
可见,只要知道了两个电压之比也就知道了两个三端电容的直接电容之比,于是就可以准确测量传感器相应的位移。两个电压源如果用感应耦合比率臂来实现,端钮对屏蔽的导纳对测量结果将没有明显的影响,因为Y23、Y’23在电路不平衡时只影响灵敏度,而当线路达到平衡状态时就没有影响了。至于Y13、Y’13引起的分压误差,则可以得到极大的降低,只要信号源的内阻足够小即可。如前所述,感应耦合比较率臂正好具有这一优良特性。
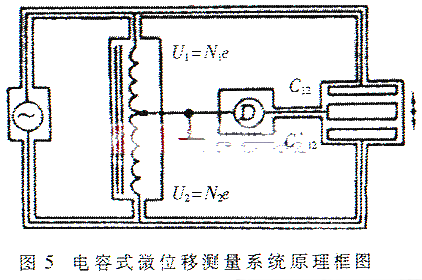 现以设计一个测量微小位移的系统为例来说明上述测量方法的应用。首先,用高导磁率环形铁芯绕制出感应耦合比率臂,再设计适当的可变间距三电极差动式电容位移传感器的结构,并采用比率测量线路,就有如图5所示的微位移测量系统原理框图。对双极板电容传感器,不考虑电场的边缘效率,两个直接电容为:C12=[(εA1)/(3.6πd1)](pF),C’12=[(εA2)/(3.6πd1)](pF)。不失一般性,对两个差动电容器可假定极板相对面积相等,即A1=A2=A(cm2)。极板间介质的介电常数也有ε1=ε2=ε(譬如均为空气)。d1、d2(cm)分别为两传感器的极板间距。N1、N2系感应分压器两部分电压对应的匝数,N1+N2=N0。将两个电容表示式代入(5)式,可得:
d1=KN1 (6)
d2=K(N0-N1) (7)
式中,K=(d1+d2)/N1+N2为测量系统的灵敏度系数,表示比率臂单位读数变化所对应的传感器中心电极的位移。现估算一下这个测量系统可能达到的指标。感应耦合比率臂的总的分压比不难做到1/N0=10 -7,两个传感器极板间距之和是个常量,取d1+d2=1mm,则位移灵敏度系数K=10 -8cm,只有0.4纳米。N1为仪器面板上的读数,其变化范围为从0到N0。
从最后获得的极板位移与比率变压器读数的关系式(6)可知,读数随中心电极的位移呈线性变化。实际完成的系统由于结构的不完善性,在接近量程的两端会出现一定程度的非线性,如果采取等电位屏蔽等措施,可以把输出特性的非线性降低到可以忽略的程度。可见,将差动式电容位移传感器与比率测量方法结合起来,设计的测量系统既有很高的分辨能力及较强的抗干扰能力,也能够获得很好的线性响应。
现以设计一个测量微小位移的系统为例来说明上述测量方法的应用。首先,用高导磁率环形铁芯绕制出感应耦合比率臂,再设计适当的可变间距三电极差动式电容位移传感器的结构,并采用比率测量线路,就有如图5所示的微位移测量系统原理框图。对双极板电容传感器,不考虑电场的边缘效率,两个直接电容为:C12=[(εA1)/(3.6πd1)](pF),C’12=[(εA2)/(3.6πd1)](pF)。不失一般性,对两个差动电容器可假定极板相对面积相等,即A1=A2=A(cm2)。极板间介质的介电常数也有ε1=ε2=ε(譬如均为空气)。d1、d2(cm)分别为两传感器的极板间距。N1、N2系感应分压器两部分电压对应的匝数,N1+N2=N0。将两个电容表示式代入(5)式,可得:
d1=KN1 (6)
d2=K(N0-N1) (7)
式中,K=(d1+d2)/N1+N2为测量系统的灵敏度系数,表示比率臂单位读数变化所对应的传感器中心电极的位移。现估算一下这个测量系统可能达到的指标。感应耦合比率臂的总的分压比不难做到1/N0=10 -7,两个传感器极板间距之和是个常量,取d1+d2=1mm,则位移灵敏度系数K=10 -8cm,只有0.4纳米。N1为仪器面板上的读数,其变化范围为从0到N0。
从最后获得的极板位移与比率变压器读数的关系式(6)可知,读数随中心电极的位移呈线性变化。实际完成的系统由于结构的不完善性,在接近量程的两端会出现一定程度的非线性,如果采取等电位屏蔽等措施,可以把输出特性的非线性降低到可以忽略的程度。可见,将差动式电容位移传感器与比率测量方法结合起来,设计的测量系统既有很高的分辨能力及较强的抗干扰能力,也能够获得很好的线性响应。
 3 实验验证
在设计之初,一般要考虑下述几个方面的问题:量程、灵敏度、精度与标准、线性、长期稳定性、频率响应与环境变化的影响系数等。结合地珠科学观测的需要,按照第三节中提出的设计方案研制了不同用途的多种测量系统。譬如研制了一个位移测量系统,量程为%26;#177;0.3毫米,分辨力可达0.02纳米,输出线性度优于0.5%,系统稳定度好于0.1纳米/日。下面简要介绍传感器与测量仪器的设计和构成以及主要的测试结果。
首先选择合适的材料。除弹簧片与绝缘材料外,电容位移传感器的所有部件均是用国产低膨胀合金4J32或4J36加工制作的,材料的线膨胀系数分别为α≤1.2~1.5%26;#215;10 -6/℃或1.8%26;#215;10 -6/℃。各部件加工后进行热处理以消除余应力,传感器组装完成后还要作时效老化处理。陶瓷绝缘材料在使用前应仔细烘干,以提高极板间的绝缘强度,降低损耗。在设计精密小位移测量传感器时要尽量采用整体结构。涉及零件装配问题时,注意设计合适的紧固螺钉位置,以期将传感器结构的蠕变减至最小。需要组合的部件,其接触面应进行研磨,从而达到稳定可靠的接触状态。
基于感应耦合比率臂的测量仪器原理框图如图5所示。为降低系统的电气噪声,一千赫兹点频信号源具有稳频、稳幅的特性。检测单元中前置放大器应尽量靠近传感器,这可以有效地提高电桥线路的输出信号电平与信噪比。一般情况下,噪声与放大器带宽成正比,故放大电路的通频带应限制到尽可能窄的程度,相敏检波技术能够足够跟踪信号源激励频率,并且保持极低的通频带。关于这方面的问题,在此不再讨论。
3 实验验证
在设计之初,一般要考虑下述几个方面的问题:量程、灵敏度、精度与标准、线性、长期稳定性、频率响应与环境变化的影响系数等。结合地珠科学观测的需要,按照第三节中提出的设计方案研制了不同用途的多种测量系统。譬如研制了一个位移测量系统,量程为%26;#177;0.3毫米,分辨力可达0.02纳米,输出线性度优于0.5%,系统稳定度好于0.1纳米/日。下面简要介绍传感器与测量仪器的设计和构成以及主要的测试结果。
首先选择合适的材料。除弹簧片与绝缘材料外,电容位移传感器的所有部件均是用国产低膨胀合金4J32或4J36加工制作的,材料的线膨胀系数分别为α≤1.2~1.5%26;#215;10 -6/℃或1.8%26;#215;10 -6/℃。各部件加工后进行热处理以消除余应力,传感器组装完成后还要作时效老化处理。陶瓷绝缘材料在使用前应仔细烘干,以提高极板间的绝缘强度,降低损耗。在设计精密小位移测量传感器时要尽量采用整体结构。涉及零件装配问题时,注意设计合适的紧固螺钉位置,以期将传感器结构的蠕变减至最小。需要组合的部件,其接触面应进行研磨,从而达到稳定可靠的接触状态。
基于感应耦合比率臂的测量仪器原理框图如图5所示。为降低系统的电气噪声,一千赫兹点频信号源具有稳频、稳幅的特性。检测单元中前置放大器应尽量靠近传感器,这可以有效地提高电桥线路的输出信号电平与信噪比。一般情况下,噪声与放大器带宽成正比,故放大电路的通频带应限制到尽可能窄的程度,相敏检波技术能够足够跟踪信号源激励频率,并且保持极低的通频带。关于这方面的问题,在此不再讨论。
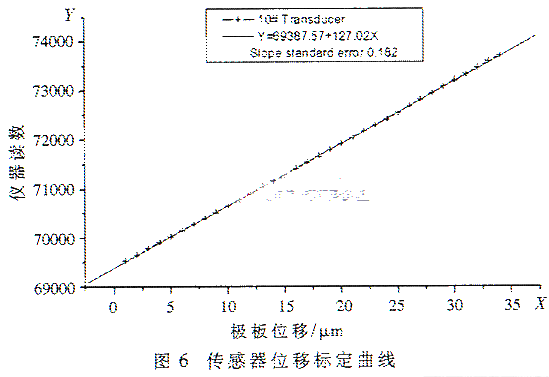
 所设计的测量系统有一个五级的感应耦合比率部件,通过调节感应耦合比率臂各档的开关位置,能够使变压器电桥系统达到或者接近平衡状态,这样可以获得较高的测量精度。但是在科学测量及生产过程中,有时需要监测位移在某个量值附近的连续变化,或者需要监测某种低频微幅振动,如若采用手动调节、平衡读数的方法,就不能满足要求了。将相敏检波器的输出经放大后接到数据采集器输入端,记录测量系统偏离平衡点的电压大小能够达到此目的,使用微动测量台架标定传感器,测值稳定,复杂性好,所获得的10号传感器位移标定曲线示如图6。图中的直线是线性拟合的结果。
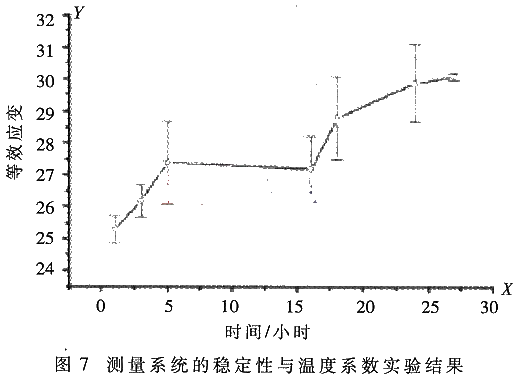
拟合方程显示在图中上部的方框图。从实验结果可看出,一微米位移可获得变压器电桥读数,变化为127.02,输出特性的非性线误差小于0.15%F.S。比率臂第五档变化一个数对应的位移量根据传感器结构的不同,一般在5~8纳米之间,末级的数据采集器可获得300多毫伏的输出,从数据采集器便能够分辨出0.02纳米的变化。在实验室环境下,传感器测值随着温度的变化会产生极大的漂移,用标准元件来检查变压器电桥测量系统的温度系数与稳定性,所得结果见图7。在28小时的实验期间测值等效变化仅为0.1纳米,环境温度变化为3~4℃。作者还曾将差动电容式位移传感器放到100米深的钻井底部,那里温度的年变化不到0.03℃,整个位移测量系统用漂移率仅为0.1纳米。
本文讨论的设计方案多年以来一直被应用于研制各种地球科学观测仪器中,有的测量系统已经在观测台站工作近二十年,获得了非常有价值的资料。该设计方案在诸如微机械加工、次声监测和精密仪器系统的设计领域有广泛的应用前景。
所设计的测量系统有一个五级的感应耦合比率部件,通过调节感应耦合比率臂各档的开关位置,能够使变压器电桥系统达到或者接近平衡状态,这样可以获得较高的测量精度。但是在科学测量及生产过程中,有时需要监测位移在某个量值附近的连续变化,或者需要监测某种低频微幅振动,如若采用手动调节、平衡读数的方法,就不能满足要求了。将相敏检波器的输出经放大后接到数据采集器输入端,记录测量系统偏离平衡点的电压大小能够达到此目的,使用微动测量台架标定传感器,测值稳定,复杂性好,所获得的10号传感器位移标定曲线示如图6。图中的直线是线性拟合的结果。
拟合方程显示在图中上部的方框图。从实验结果可看出,一微米位移可获得变压器电桥读数,变化为127.02,输出特性的非性线误差小于0.15%F.S。比率臂第五档变化一个数对应的位移量根据传感器结构的不同,一般在5~8纳米之间,末级的数据采集器可获得300多毫伏的输出,从数据采集器便能够分辨出0.02纳米的变化。在实验室环境下,传感器测值随着温度的变化会产生极大的漂移,用标准元件来检查变压器电桥测量系统的温度系数与稳定性,所得结果见图7。在28小时的实验期间测值等效变化仅为0.1纳米,环境温度变化为3~4℃。作者还曾将差动电容式位移传感器放到100米深的钻井底部,那里温度的年变化不到0.03℃,整个位移测量系统用漂移率仅为0.1纳米。
本文讨论的设计方案多年以来一直被应用于研制各种地球科学观测仪器中,有的测量系统已经在观测台站工作近二十年,获得了非常有价值的资料。该设计方案在诸如微机械加工、次声监测和精密仪器系统的设计领域有广泛的应用前景。
引用地址:基于感应耦合比率臂的高精度位移测量系统
 1 比率测量法
一个物理量f,其值取决于外界因素如t(温度)、u(电压)……等,其一阶展开式为:
f=f0+(аf/аt)0Δt+(аf/аu)0Δu+A (1)
为简化数字运算,只考虑存在一个干扰因素的情况,参考量f1与被测量f2可以分别写作:f1=f01(1+β1Δt)和f2=f02(1+β2Δt),此处β1=1/(f01)(аf1)/(аt)0, β2=1/(f02)[(аf2)/(аt)]0,且有β1Δt<<1,β2Δt<<1。容易求出上述三种方法中的相对测量误差各为:
а绝对=β2Δt=Lβ1ΔT (2)
а差值=[(f02β2-f01β1)Δt/(f02-f01)]=[(LK-1)/(K-1)]β1ΔT (3)
а比率=(β2-β1) Δt=(L-1)β1Δt (4)
1 比率测量法
一个物理量f,其值取决于外界因素如t(温度)、u(电压)……等,其一阶展开式为:
f=f0+(аf/аt)0Δt+(аf/аu)0Δu+A (1)
为简化数字运算,只考虑存在一个干扰因素的情况,参考量f1与被测量f2可以分别写作:f1=f01(1+β1Δt)和f2=f02(1+β2Δt),此处β1=1/(f01)(аf1)/(аt)0, β2=1/(f02)[(аf2)/(аt)]0,且有β1Δt<<1,β2Δt<<1。容易求出上述三种方法中的相对测量误差各为:
а绝对=β2Δt=Lβ1ΔT (2)
а差值=[(f02β2-f01β1)Δt/(f02-f01)]=[(LK-1)/(K-1)]β1ΔT (3)
а比率=(β2-β1) Δt=(L-1)β1Δt (4)
 其中L=(β2)/(β1),K=(f02)/(f01)。图1表示取L=1.5时相对误差随元件值的分布情况。可以看出,比率测量法在很宽的测量范围内均具有良好的抗干扰能力。当存在多个影响因素或者在分析由上述方法组合成的测量装置时,可根据叠加原理按系统误差的理论综合评定其精度。
2 电容位移传感器与比率测量
电容式微小位测量系统是近年来发展最快的位移测量技术之一。众所周知,用两块平行的金属板就可以构成一个电容位移传感器,其电容量由极板的相对有效面积、极板间距以及填充的介质特性所决定。只要被测特体位置的移动改变了电容器上述任何一个结构参数,传感器的电容量就会发生变化,通过测量电容量的变动即可精确地知道特体位移的大小。
其中L=(β2)/(β1),K=(f02)/(f01)。图1表示取L=1.5时相对误差随元件值的分布情况。可以看出,比率测量法在很宽的测量范围内均具有良好的抗干扰能力。当存在多个影响因素或者在分析由上述方法组合成的测量装置时,可根据叠加原理按系统误差的理论综合评定其精度。
2 电容位移传感器与比率测量
电容式微小位测量系统是近年来发展最快的位移测量技术之一。众所周知,用两块平行的金属板就可以构成一个电容位移传感器,其电容量由极板的相对有效面积、极板间距以及填充的介质特性所决定。只要被测特体位置的移动改变了电容器上述任何一个结构参数,传感器的电容量就会发生变化,通过测量电容量的变动即可精确地知道特体位移的大小。
 电容位移传感器的三种基本类型如图2所示。其具体结构可视实际运用的场合灵活多变,电容极板可以是平面的或者球面的;运行电极可以采用水银等导电液体。图2所示的三种基本类型均可组成差动式结构,如各分类中下部图形所示。采用差动式结构能够提高传感器线路的输出灵敏度,减小非线性,还能在一定程序上抑制由静电吸引带来的误差。当要求测量系统具有很高的分辨力时,一般是保持极板面积相对固定而使电容传感器极板间隙随被测位移改变,即如图2(a)所示的结构。反之,采用保持间隔恒定而让极板相对面积可变的结构,则可以在相当大的动态范围内获得线性的响应。
一般情况下,电阻、电感和电容等电子元件均被盾作双端元件。两端电容器的等效电路示如图3(a)。由于各端钮对附近导电物体的分布电容C1G、C2G是变化的,所以其总电容C12+[(C1G%26;#215;C2G)/(C1G+C2G)也是不稳定的。如果电容式传位移传感设计成这种简单的结构,外界干扰会很大。为了消除上述分布参数的影响,必须对电容传感器进行完善的静电屏蔽,形成如图3(b)的结构,称之为三端电容器。这样的三端电容元件中,由极板形成的直接电容C12是确定的,但是C13、C23仍受引线芯屏间电容的影响。如何排队三端电容中分布参数的影响?怎样准确测量与位移相关的直接电容的大小呢?
电容位移传感器的三种基本类型如图2所示。其具体结构可视实际运用的场合灵活多变,电容极板可以是平面的或者球面的;运行电极可以采用水银等导电液体。图2所示的三种基本类型均可组成差动式结构,如各分类中下部图形所示。采用差动式结构能够提高传感器线路的输出灵敏度,减小非线性,还能在一定程序上抑制由静电吸引带来的误差。当要求测量系统具有很高的分辨力时,一般是保持极板面积相对固定而使电容传感器极板间隙随被测位移改变,即如图2(a)所示的结构。反之,采用保持间隔恒定而让极板相对面积可变的结构,则可以在相当大的动态范围内获得线性的响应。
一般情况下,电阻、电感和电容等电子元件均被盾作双端元件。两端电容器的等效电路示如图3(a)。由于各端钮对附近导电物体的分布电容C1G、C2G是变化的,所以其总电容C12+[(C1G%26;#215;C2G)/(C1G+C2G)也是不稳定的。如果电容式传位移传感设计成这种简单的结构,外界干扰会很大。为了消除上述分布参数的影响,必须对电容传感器进行完善的静电屏蔽,形成如图3(b)的结构,称之为三端电容器。这样的三端电容元件中,由极板形成的直接电容C12是确定的,但是C13、C23仍受引线芯屏间电容的影响。如何排队三端电容中分布参数的影响?怎样准确测量与位移相关的直接电容的大小呢?
 上世纪五十年代在电力工学和计算学领域出现了一种新型的电压比率器件——感应耦合比率臂,它的突出特点是分压精度高,可达10 -8量级以上;输出阻抗低,能做到10mΩ以下;长期稳定性非常好,年漂移率保持在10 -9的水平。其后,感应分压器的理论与工艺日臻完善,极大地提高了电工测量和标准计量的精度,实现了对小电容的高精度测量,进而以计算电容与感应分压器为基准导出了电阻、电感等的计量标准。这一成就也对精密测量领域产生了积极的推动作用。
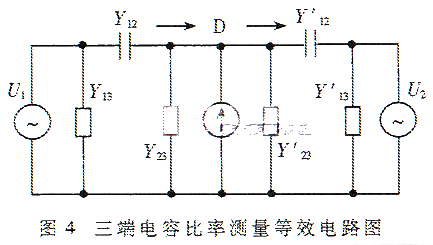
如果将两个三端电容串接起来,分别用两个信号源供电,就形成了如图4所示的等效电路,其中,Y12=jωC12,Y’12=jωC"12。在公共点D与接地端之间连接一个检流计,调节两个外加电压的幅值和相位,使通过两个直接电容流向D点的电流大小相等、方向相反,直道检流计指零,便可得到下面的关系式:
C12/C’12=-(U2/U1) (5)
可见,只要知道了两个电压之比也就知道了两个三端电容的直接电容之比,于是就可以准确测量传感器相应的位移。两个电压源如果用感应耦合比率臂来实现,端钮对屏蔽的导纳对测量结果将没有明显的影响,因为Y23、Y’23在电路不平衡时只影响灵敏度,而当线路达到平衡状态时就没有影响了。至于Y13、Y’13引起的分压误差,则可以得到极大的降低,只要信号源的内阻足够小即可。如前所述,感应耦合比较率臂正好具有这一优良特性。
上世纪五十年代在电力工学和计算学领域出现了一种新型的电压比率器件——感应耦合比率臂,它的突出特点是分压精度高,可达10 -8量级以上;输出阻抗低,能做到10mΩ以下;长期稳定性非常好,年漂移率保持在10 -9的水平。其后,感应分压器的理论与工艺日臻完善,极大地提高了电工测量和标准计量的精度,实现了对小电容的高精度测量,进而以计算电容与感应分压器为基准导出了电阻、电感等的计量标准。这一成就也对精密测量领域产生了积极的推动作用。
如果将两个三端电容串接起来,分别用两个信号源供电,就形成了如图4所示的等效电路,其中,Y12=jωC12,Y’12=jωC"12。在公共点D与接地端之间连接一个检流计,调节两个外加电压的幅值和相位,使通过两个直接电容流向D点的电流大小相等、方向相反,直道检流计指零,便可得到下面的关系式:
C12/C’12=-(U2/U1) (5)
可见,只要知道了两个电压之比也就知道了两个三端电容的直接电容之比,于是就可以准确测量传感器相应的位移。两个电压源如果用感应耦合比率臂来实现,端钮对屏蔽的导纳对测量结果将没有明显的影响,因为Y23、Y’23在电路不平衡时只影响灵敏度,而当线路达到平衡状态时就没有影响了。至于Y13、Y’13引起的分压误差,则可以得到极大的降低,只要信号源的内阻足够小即可。如前所述,感应耦合比较率臂正好具有这一优良特性。
 现以设计一个测量微小位移的系统为例来说明上述测量方法的应用。首先,用高导磁率环形铁芯绕制出感应耦合比率臂,再设计适当的可变间距三电极差动式电容位移传感器的结构,并采用比率测量线路,就有如图5所示的微位移测量系统原理框图。对双极板电容传感器,不考虑电场的边缘效率,两个直接电容为:C12=[(εA1)/(3.6πd1)](pF),C’12=[(εA2)/(3.6πd1)](pF)。不失一般性,对两个差动电容器可假定极板相对面积相等,即A1=A2=A(cm2)。极板间介质的介电常数也有ε1=ε2=ε(譬如均为空气)。d1、d2(cm)分别为两传感器的极板间距。N1、N2系感应分压器两部分电压对应的匝数,N1+N2=N0。将两个电容表示式代入(5)式,可得:
d1=KN1 (6)
d2=K(N0-N1) (7)
式中,K=(d1+d2)/N1+N2为测量系统的灵敏度系数,表示比率臂单位读数变化所对应的传感器中心电极的位移。现估算一下这个测量系统可能达到的指标。感应耦合比率臂的总的分压比不难做到1/N0=10 -7,两个传感器极板间距之和是个常量,取d1+d2=1mm,则位移灵敏度系数K=10 -8cm,只有0.4纳米。N1为仪器面板上的读数,其变化范围为从0到N0。
从最后获得的极板位移与比率变压器读数的关系式(6)可知,读数随中心电极的位移呈线性变化。实际完成的系统由于结构的不完善性,在接近量程的两端会出现一定程度的非线性,如果采取等电位屏蔽等措施,可以把输出特性的非线性降低到可以忽略的程度。可见,将差动式电容位移传感器与比率测量方法结合起来,设计的测量系统既有很高的分辨能力及较强的抗干扰能力,也能够获得很好的线性响应。
现以设计一个测量微小位移的系统为例来说明上述测量方法的应用。首先,用高导磁率环形铁芯绕制出感应耦合比率臂,再设计适当的可变间距三电极差动式电容位移传感器的结构,并采用比率测量线路,就有如图5所示的微位移测量系统原理框图。对双极板电容传感器,不考虑电场的边缘效率,两个直接电容为:C12=[(εA1)/(3.6πd1)](pF),C’12=[(εA2)/(3.6πd1)](pF)。不失一般性,对两个差动电容器可假定极板相对面积相等,即A1=A2=A(cm2)。极板间介质的介电常数也有ε1=ε2=ε(譬如均为空气)。d1、d2(cm)分别为两传感器的极板间距。N1、N2系感应分压器两部分电压对应的匝数,N1+N2=N0。将两个电容表示式代入(5)式,可得:
d1=KN1 (6)
d2=K(N0-N1) (7)
式中,K=(d1+d2)/N1+N2为测量系统的灵敏度系数,表示比率臂单位读数变化所对应的传感器中心电极的位移。现估算一下这个测量系统可能达到的指标。感应耦合比率臂的总的分压比不难做到1/N0=10 -7,两个传感器极板间距之和是个常量,取d1+d2=1mm,则位移灵敏度系数K=10 -8cm,只有0.4纳米。N1为仪器面板上的读数,其变化范围为从0到N0。
从最后获得的极板位移与比率变压器读数的关系式(6)可知,读数随中心电极的位移呈线性变化。实际完成的系统由于结构的不完善性,在接近量程的两端会出现一定程度的非线性,如果采取等电位屏蔽等措施,可以把输出特性的非线性降低到可以忽略的程度。可见,将差动式电容位移传感器与比率测量方法结合起来,设计的测量系统既有很高的分辨能力及较强的抗干扰能力,也能够获得很好的线性响应。
 3 实验验证
在设计之初,一般要考虑下述几个方面的问题:量程、灵敏度、精度与标准、线性、长期稳定性、频率响应与环境变化的影响系数等。结合地珠科学观测的需要,按照第三节中提出的设计方案研制了不同用途的多种测量系统。譬如研制了一个位移测量系统,量程为%26;#177;0.3毫米,分辨力可达0.02纳米,输出线性度优于0.5%,系统稳定度好于0.1纳米/日。下面简要介绍传感器与测量仪器的设计和构成以及主要的测试结果。
首先选择合适的材料。除弹簧片与绝缘材料外,电容位移传感器的所有部件均是用国产低膨胀合金4J32或4J36加工制作的,材料的线膨胀系数分别为α≤1.2~1.5%26;#215;10 -6/℃或1.8%26;#215;10 -6/℃。各部件加工后进行热处理以消除余应力,传感器组装完成后还要作时效老化处理。陶瓷绝缘材料在使用前应仔细烘干,以提高极板间的绝缘强度,降低损耗。在设计精密小位移测量传感器时要尽量采用整体结构。涉及零件装配问题时,注意设计合适的紧固螺钉位置,以期将传感器结构的蠕变减至最小。需要组合的部件,其接触面应进行研磨,从而达到稳定可靠的接触状态。
基于感应耦合比率臂的测量仪器原理框图如图5所示。为降低系统的电气噪声,一千赫兹点频信号源具有稳频、稳幅的特性。检测单元中前置放大器应尽量靠近传感器,这可以有效地提高电桥线路的输出信号电平与信噪比。一般情况下,噪声与放大器带宽成正比,故放大电路的通频带应限制到尽可能窄的程度,相敏检波技术能够足够跟踪信号源激励频率,并且保持极低的通频带。关于这方面的问题,在此不再讨论。
3 实验验证
在设计之初,一般要考虑下述几个方面的问题:量程、灵敏度、精度与标准、线性、长期稳定性、频率响应与环境变化的影响系数等。结合地珠科学观测的需要,按照第三节中提出的设计方案研制了不同用途的多种测量系统。譬如研制了一个位移测量系统,量程为%26;#177;0.3毫米,分辨力可达0.02纳米,输出线性度优于0.5%,系统稳定度好于0.1纳米/日。下面简要介绍传感器与测量仪器的设计和构成以及主要的测试结果。
首先选择合适的材料。除弹簧片与绝缘材料外,电容位移传感器的所有部件均是用国产低膨胀合金4J32或4J36加工制作的,材料的线膨胀系数分别为α≤1.2~1.5%26;#215;10 -6/℃或1.8%26;#215;10 -6/℃。各部件加工后进行热处理以消除余应力,传感器组装完成后还要作时效老化处理。陶瓷绝缘材料在使用前应仔细烘干,以提高极板间的绝缘强度,降低损耗。在设计精密小位移测量传感器时要尽量采用整体结构。涉及零件装配问题时,注意设计合适的紧固螺钉位置,以期将传感器结构的蠕变减至最小。需要组合的部件,其接触面应进行研磨,从而达到稳定可靠的接触状态。
基于感应耦合比率臂的测量仪器原理框图如图5所示。为降低系统的电气噪声,一千赫兹点频信号源具有稳频、稳幅的特性。检测单元中前置放大器应尽量靠近传感器,这可以有效地提高电桥线路的输出信号电平与信噪比。一般情况下,噪声与放大器带宽成正比,故放大电路的通频带应限制到尽可能窄的程度,相敏检波技术能够足够跟踪信号源激励频率,并且保持极低的通频带。关于这方面的问题,在此不再讨论。
 所设计的测量系统有一个五级的感应耦合比率部件,通过调节感应耦合比率臂各档的开关位置,能够使变压器电桥系统达到或者接近平衡状态,这样可以获得较高的测量精度。但是在科学测量及生产过程中,有时需要监测位移在某个量值附近的连续变化,或者需要监测某种低频微幅振动,如若采用手动调节、平衡读数的方法,就不能满足要求了。将相敏检波器的输出经放大后接到数据采集器输入端,记录测量系统偏离平衡点的电压大小能够达到此目的,使用微动测量台架标定传感器,测值稳定,复杂性好,所获得的10号传感器位移标定曲线示如图6。图中的直线是线性拟合的结果。
拟合方程显示在图中上部的方框图。从实验结果可看出,一微米位移可获得变压器电桥读数,变化为127.02,输出特性的非性线误差小于0.15%F.S。比率臂第五档变化一个数对应的位移量根据传感器结构的不同,一般在5~8纳米之间,末级的数据采集器可获得300多毫伏的输出,从数据采集器便能够分辨出0.02纳米的变化。在实验室环境下,传感器测值随着温度的变化会产生极大的漂移,用标准元件来检查变压器电桥测量系统的温度系数与稳定性,所得结果见图7。在28小时的实验期间测值等效变化仅为0.1纳米,环境温度变化为3~4℃。作者还曾将差动电容式位移传感器放到100米深的钻井底部,那里温度的年变化不到0.03℃,整个位移测量系统用漂移率仅为0.1纳米。
本文讨论的设计方案多年以来一直被应用于研制各种地球科学观测仪器中,有的测量系统已经在观测台站工作近二十年,获得了非常有价值的资料。该设计方案在诸如微机械加工、次声监测和精密仪器系统的设计领域有广泛的应用前景。
所设计的测量系统有一个五级的感应耦合比率部件,通过调节感应耦合比率臂各档的开关位置,能够使变压器电桥系统达到或者接近平衡状态,这样可以获得较高的测量精度。但是在科学测量及生产过程中,有时需要监测位移在某个量值附近的连续变化,或者需要监测某种低频微幅振动,如若采用手动调节、平衡读数的方法,就不能满足要求了。将相敏检波器的输出经放大后接到数据采集器输入端,记录测量系统偏离平衡点的电压大小能够达到此目的,使用微动测量台架标定传感器,测值稳定,复杂性好,所获得的10号传感器位移标定曲线示如图6。图中的直线是线性拟合的结果。
拟合方程显示在图中上部的方框图。从实验结果可看出,一微米位移可获得变压器电桥读数,变化为127.02,输出特性的非性线误差小于0.15%F.S。比率臂第五档变化一个数对应的位移量根据传感器结构的不同,一般在5~8纳米之间,末级的数据采集器可获得300多毫伏的输出,从数据采集器便能够分辨出0.02纳米的变化。在实验室环境下,传感器测值随着温度的变化会产生极大的漂移,用标准元件来检查变压器电桥测量系统的温度系数与稳定性,所得结果见图7。在28小时的实验期间测值等效变化仅为0.1纳米,环境温度变化为3~4℃。作者还曾将差动电容式位移传感器放到100米深的钻井底部,那里温度的年变化不到0.03℃,整个位移测量系统用漂移率仅为0.1纳米。
本文讨论的设计方案多年以来一直被应用于研制各种地球科学观测仪器中,有的测量系统已经在观测台站工作近二十年,获得了非常有价值的资料。该设计方案在诸如微机械加工、次声监测和精密仪器系统的设计领域有广泛的应用前景。 
 硬件架构艺术:数字电路的设计方法与技术
硬件架构艺术:数字电路的设计方法与技术 ICL7612ACPA
ICL7612ACPA










 京公网安备 11010802033920号
京公网安备 11010802033920号