摘要:矩阵变换器具有一系列的优点,已成为交-交变换器研究中非常热门的课题,但其电压传输比一直比较低。针对矩阵变换器在目前的拓扑结构下最大的电压传输比仅为0.866,提出了"泵式"矩阵变换器,分析了它的拓扑结构和工作原理,并进行了Matlab仿真,实现了电压传输比的提高。
关键词:电压增益 矩阵变换器 Matlab仿真
矩阵变换器具有一系列优点,但迟迟不能进入实用阶段,其重要的原因之一就在于它的电压传输比比较低。
在现有矩阵变换器的拓扑结构与调制策略基础上,得到的输出输入电压传输比都小于等于1[1~3]。通过对矩阵变换器电压传输比进行严格的数学证明可知:在希望得到输出相电压为正弦电压的情况下,最大传输比为0.866[4]。虽然对现有的调制策略进行修正和改进在一定程度上可以提高电压传输比,但仍难以达到期望效果。若还局限于现有的拓扑结构,那么将很难进一步提高电压传输比。只有突破原有矩阵变换器拓扑结构并采取相应的调制策略,才有可能进一步提高电压传输比。于是,本文提出了"泵式"单相矩阵变换器的拓扑结构和相应的调制策略,即采用一个与往复式机械泵机理相似的矩阵变换器拓扑结构,并将高频升压与斩波与斩波调制协调配合实现双向调压,从而使得总电压传输比大于1。
图1
1 "泵式"矩阵变换器的拓扑结构和工作过程
1.1拓扑结构
“泵式”矩阵变换器的基本拓扑结构[5]如图1所示,其中,S11、S12、S21、S22、S0均为无延时的理想双向功率开关管,L1、C1、L2、C2均工作在高频斩波状态。
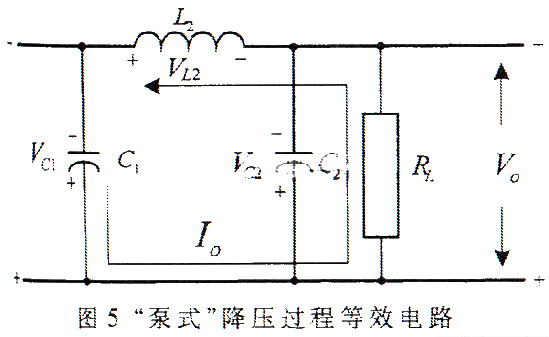
开关管S11、S12、S21、S22共同构成开关矩阵,其对应调制矩阵为:
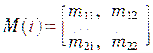 1.2"泵"式矩阵变换器的工作原理
矩阵式变换器可以实现交流电诸参数(相数、相位、幅值、频率)的变换。实现参数变换的过程,就是建立一个对应于开关矩阵(如图1 S11、S12、S21所示)的M(t)调制矩阵,并通过实时运算得出M(t)调制矩阵内矩阵因子的数值,从而控制矩阵变换器上相应功率开关管的导通时间。在每个斩波周期内,通过开关管的不同通断状态组合,实现对输出参数的控制。
“泵”式矩阵变换器各开关管的工作规律是由M(t)调制矩阵内矩阵因子决定的,矩阵因子mij(i=1,2; j=1,2)为相应双向开关管的占空比。现以图1中开关管S0、S11、S22、S12、 S21的工作状态说明"泵"式矩阵变换器的工作原理。在这里,S状态:"1"表示该开关管导通,"0"表示该开关管关断。
对于图1电路,输入/输出电压的关系可表示为:
1.2"泵"式矩阵变换器的工作原理
矩阵式变换器可以实现交流电诸参数(相数、相位、幅值、频率)的变换。实现参数变换的过程,就是建立一个对应于开关矩阵(如图1 S11、S12、S21所示)的M(t)调制矩阵,并通过实时运算得出M(t)调制矩阵内矩阵因子的数值,从而控制矩阵变换器上相应功率开关管的导通时间。在每个斩波周期内,通过开关管的不同通断状态组合,实现对输出参数的控制。
“泵”式矩阵变换器各开关管的工作规律是由M(t)调制矩阵内矩阵因子决定的,矩阵因子mij(i=1,2; j=1,2)为相应双向开关管的占空比。现以图1中开关管S0、S11、S22、S12、 S21的工作状态说明"泵"式矩阵变换器的工作原理。在这里,S状态:"1"表示该开关管导通,"0"表示该开关管关断。
对于图1电路,输入/输出电压的关系可表示为:
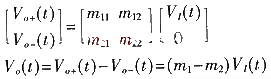
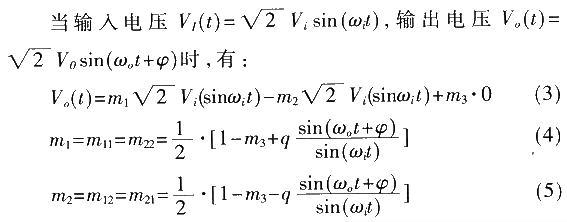 式中,ωi为输入频率,ωo为输出频率,ψ为输出初相角,q=Vo/Vi.
通常,一个斩波周期T包含三个时段:S11和S22、导通,S12和S21关断的T1时段;S11和S22关断、S12和S21导通的T2时段;S11、S22、S12和S21都导通的T3时段。且有T1、T2、T3=T,m1+m2+m3=1,m1=m11=m22,m2=m12=m21。
“泵”式矩阵变换器的工作过程包含以下两步:
①在斩波周期T中的(T1+T2)时段,S0导通,等值线路如图2所标,分为两个独立回路:
回路a ,T1电流值上升,从电网吸收能量;
式中,ωi为输入频率,ωo为输出频率,ψ为输出初相角,q=Vo/Vi.
通常,一个斩波周期T包含三个时段:S11和S22、导通,S12和S21关断的T1时段;S11和S22关断、S12和S21导通的T2时段;S11、S22、S12和S21都导通的T3时段。且有T1、T2、T3=T,m1+m2+m3=1,m1=m11=m22,m2=m12=m21。
“泵”式矩阵变换器的工作过程包含以下两步:
①在斩波周期T中的(T1+T2)时段,S0导通,等值线路如图2所标,分为两个独立回路:
回路a ,T1电流值上升,从电网吸收能量;
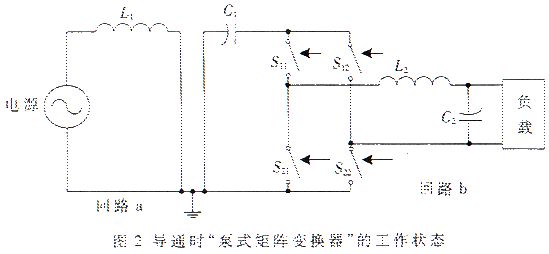 回路b--C1上的电压VC1(t)作为开关管矩阵的电源为负载提供能量。
在这段时间内,对开关矩阵而言又分为两个工作时段,即T1和T2。在T1时段内,S11和S22导通;在T2时段内,S21和S12导通。这里,根据T1/T2的变化,可以实现对波形的调制。
②在斩波周期T的T3时段,S0截止,等值电路如图3所示,同样也由两个独立回路构成:
回路a--L1释放能量,电源和L1趾联对C1充电,适当选择T3可使电容C1的充电电压VC1(t)大于电源电压,从而实现了"电压提升"。
回路b--S11、S12、S21、S22同时导通,可以等效为一个导通的SM,感性负载续流。
图3
要特别注意:此时开关矩阵并未直接与电源连接,因此S11、S12、S21和S22同时导通不会引起输入电源短路,感性负载通过它们提供的回路也不会出现过电压。
在泵式矩阵变换器的工作过程中,经过T3→(T1+T2)→T3的如此往复循环,通过L1和C1便将输入电压"泵升"到电容G1上的电压VC1(t),并作为开关矩阵的输入电源,提高了开关矩阵的输入电压;与此同时,开关矩阵经过T3→T1→T2→T3的斩波循环,也完成了"波形调制"。
1.3"泵式"矩阵变换器总电压传输比Q
回路b--C1上的电压VC1(t)作为开关管矩阵的电源为负载提供能量。
在这段时间内,对开关矩阵而言又分为两个工作时段,即T1和T2。在T1时段内,S11和S22导通;在T2时段内,S21和S12导通。这里,根据T1/T2的变化,可以实现对波形的调制。
②在斩波周期T的T3时段,S0截止,等值电路如图3所示,同样也由两个独立回路构成:
回路a--L1释放能量,电源和L1趾联对C1充电,适当选择T3可使电容C1的充电电压VC1(t)大于电源电压,从而实现了"电压提升"。
回路b--S11、S12、S21、S22同时导通,可以等效为一个导通的SM,感性负载续流。
图3
要特别注意:此时开关矩阵并未直接与电源连接,因此S11、S12、S21和S22同时导通不会引起输入电源短路,感性负载通过它们提供的回路也不会出现过电压。
在泵式矩阵变换器的工作过程中,经过T3→(T1+T2)→T3的如此往复循环,通过L1和C1便将输入电压"泵升"到电容G1上的电压VC1(t),并作为开关矩阵的输入电源,提高了开关矩阵的输入电压;与此同时,开关矩阵经过T3→T1→T2→T3的斩波循环,也完成了"波形调制"。
1.3"泵式"矩阵变换器总电压传输比Q
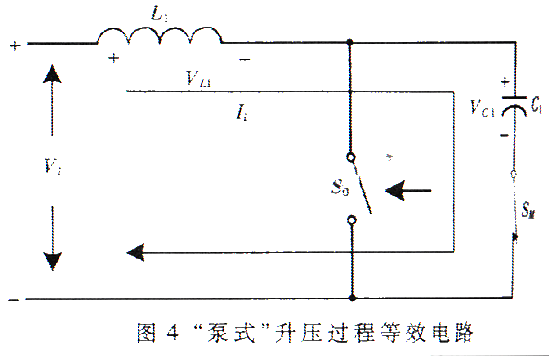 (1)升压过程
开关管S0、电感L1、电容C1组成升压回路,其等效电路如图4所示。当S0导通时,L1从V1(t)电源吸收并储存能量;当S0截止,SM导通时,电源V1(t)与L1上的电势串联,向C1充电,这时可以认为C1是升压回路的负载,此后C1两端的电压便是开关矩阵的输入电压。
升压过程的电压传输比为[5]:
(2)降压过程
电容C1、C2与电感L2以及负载组成降压回路,其等效电路如图5所示。当S0闭合时,VC1(t)成为降压部分的输入电压,电容C1向负载和储能电感L2放电使L2储能;当开关管件S0截止且SM导通时,L2向负载释放能量(续流)。
降压过程的电压传输比为[5]:g2=m1+m2
(3)"泵式电路"电压传输比
显然,“泵”式电路的电压传输比为:
由公式(8)可知:当m3<0.5时,q0>1,Vc2(t)>V1(t),"泵"式电路将工作在升压状态。
(1)升压过程
开关管S0、电感L1、电容C1组成升压回路,其等效电路如图4所示。当S0导通时,L1从V1(t)电源吸收并储存能量;当S0截止,SM导通时,电源V1(t)与L1上的电势串联,向C1充电,这时可以认为C1是升压回路的负载,此后C1两端的电压便是开关矩阵的输入电压。
升压过程的电压传输比为[5]:
(2)降压过程
电容C1、C2与电感L2以及负载组成降压回路,其等效电路如图5所示。当S0闭合时,VC1(t)成为降压部分的输入电压,电容C1向负载和储能电感L2放电使L2储能;当开关管件S0截止且SM导通时,L2向负载释放能量(续流)。
降压过程的电压传输比为[5]:g2=m1+m2
(3)"泵式电路"电压传输比
显然,“泵”式电路的电压传输比为:
由公式(8)可知:当m3<0.5时,q0>1,Vc2(t)>V1(t),"泵"式电路将工作在升压状态。
 (4)开关矩阵斩波的电压传输比q
开关矩阵工作于波形调制方式时,开关矩阵具有输入/输出电压传输比q,在实时计算调制函数时,q是人为设定的。
(5)"泵"式矩阵变换器的电源输入/矩阵输出的总电压传输比Q
“泵”式矩阵变换器的总电压传输比为“泵电路”电压传输比和“波形调制”电压传输比之积:
当斩波周期T足够小时,在相邻的几个斩波周期中,可以认为m1、m2分别为常数。而在矩阵变换器工作中,m3为预先设定的常数。通过适当选择m3和q,可使Q>1。
图6
2 "泵式"矩阵变换器的仿真实验
为验证“泵式”矩阵变换器的拓扑结构与调制策略,采用Matlab/Simulink仿真软件建立仿真模型。仿真模型包括主电路和控制电路两部分。
图6给出了在负载电阻为22Ω,负载电感为10mH,q=0.5,m3=0.7,斩波频率为10kHz,输入峰值电压为100V,频率为50Hz,输出频率为75Hz、40Hz时,"泵"式矩阵变换器的输出电压波形。从图中可以看出电压传输比均大于1。
在仿真模型中设定不同电压传输比,以验证“泵”式矩阵变换器的理论和电压传输比的相关公式。在表1中列出了幅值为100V的输入电压,经"泵"式矩阵变换器的调制后的输出电压幅值与m3、q、Q的对应关系。
表1 “泵”式矩阵变换器输入/输出比(此时输入电压幅值为100V)
q
m3
Q
仿真输出电压幅值/V
0.1
0.1
0.9
95
0.7
0.3
33
0.3
0.1
2.7
288
0.7
0.9
93
结果表明:电压传输比可以双向调节;理论计算的总传输比Q与实测结果吻合。
针对矩阵变换器的电压传输比偏低的普遍性难题,本文以单相矩阵变换器为平台,突破经典矩阵变换器的约束条件和拓扑结构,提出了一种可以实现双向调节输出电压的“泵”式矩阵变换器,其电压传输比可大于1。
在详细分析了工作过程的基础上,给出了总控制电压传输比Q的计算公式。通过Matlab/Simulink软件的仿真模型,得到多组实验数据,验证了"泵"式矩阵变换器的调制策略和有关电压传输比的分析和计算公式,获得了期望的结果。
(4)开关矩阵斩波的电压传输比q
开关矩阵工作于波形调制方式时,开关矩阵具有输入/输出电压传输比q,在实时计算调制函数时,q是人为设定的。
(5)"泵"式矩阵变换器的电源输入/矩阵输出的总电压传输比Q
“泵”式矩阵变换器的总电压传输比为“泵电路”电压传输比和“波形调制”电压传输比之积:
当斩波周期T足够小时,在相邻的几个斩波周期中,可以认为m1、m2分别为常数。而在矩阵变换器工作中,m3为预先设定的常数。通过适当选择m3和q,可使Q>1。
图6
2 "泵式"矩阵变换器的仿真实验
为验证“泵式”矩阵变换器的拓扑结构与调制策略,采用Matlab/Simulink仿真软件建立仿真模型。仿真模型包括主电路和控制电路两部分。
图6给出了在负载电阻为22Ω,负载电感为10mH,q=0.5,m3=0.7,斩波频率为10kHz,输入峰值电压为100V,频率为50Hz,输出频率为75Hz、40Hz时,"泵"式矩阵变换器的输出电压波形。从图中可以看出电压传输比均大于1。
在仿真模型中设定不同电压传输比,以验证“泵”式矩阵变换器的理论和电压传输比的相关公式。在表1中列出了幅值为100V的输入电压,经"泵"式矩阵变换器的调制后的输出电压幅值与m3、q、Q的对应关系。
表1 “泵”式矩阵变换器输入/输出比(此时输入电压幅值为100V)
q
m3
Q
仿真输出电压幅值/V
0.1
0.1
0.9
95
0.7
0.3
33
0.3
0.1
2.7
288
0.7
0.9
93
结果表明:电压传输比可以双向调节;理论计算的总传输比Q与实测结果吻合。
针对矩阵变换器的电压传输比偏低的普遍性难题,本文以单相矩阵变换器为平台,突破经典矩阵变换器的约束条件和拓扑结构,提出了一种可以实现双向调节输出电压的“泵”式矩阵变换器,其电压传输比可大于1。
在详细分析了工作过程的基础上,给出了总控制电压传输比Q的计算公式。通过Matlab/Simulink软件的仿真模型,得到多组实验数据,验证了"泵"式矩阵变换器的调制策略和有关电压传输比的分析和计算公式,获得了期望的结果。
引用地址:升压型单相矩阵变换器
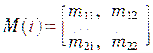 1.2"泵"式矩阵变换器的工作原理
矩阵式变换器可以实现交流电诸参数(相数、相位、幅值、频率)的变换。实现参数变换的过程,就是建立一个对应于开关矩阵(如图1 S11、S12、S21所示)的M(t)调制矩阵,并通过实时运算得出M(t)调制矩阵内矩阵因子的数值,从而控制矩阵变换器上相应功率开关管的导通时间。在每个斩波周期内,通过开关管的不同通断状态组合,实现对输出参数的控制。
“泵”式矩阵变换器各开关管的工作规律是由M(t)调制矩阵内矩阵因子决定的,矩阵因子mij(i=1,2; j=1,2)为相应双向开关管的占空比。现以图1中开关管S0、S11、S22、S12、 S21的工作状态说明"泵"式矩阵变换器的工作原理。在这里,S状态:"1"表示该开关管导通,"0"表示该开关管关断。
对于图1电路,输入/输出电压的关系可表示为:
1.2"泵"式矩阵变换器的工作原理
矩阵式变换器可以实现交流电诸参数(相数、相位、幅值、频率)的变换。实现参数变换的过程,就是建立一个对应于开关矩阵(如图1 S11、S12、S21所示)的M(t)调制矩阵,并通过实时运算得出M(t)调制矩阵内矩阵因子的数值,从而控制矩阵变换器上相应功率开关管的导通时间。在每个斩波周期内,通过开关管的不同通断状态组合,实现对输出参数的控制。
“泵”式矩阵变换器各开关管的工作规律是由M(t)调制矩阵内矩阵因子决定的,矩阵因子mij(i=1,2; j=1,2)为相应双向开关管的占空比。现以图1中开关管S0、S11、S22、S12、 S21的工作状态说明"泵"式矩阵变换器的工作原理。在这里,S状态:"1"表示该开关管导通,"0"表示该开关管关断。
对于图1电路,输入/输出电压的关系可表示为:
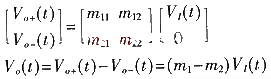
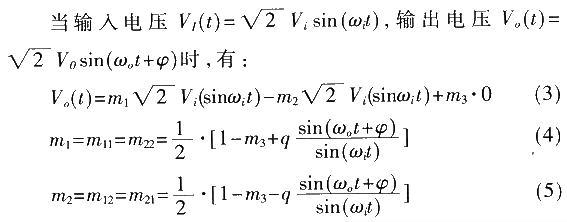 式中,ωi为输入频率,ωo为输出频率,ψ为输出初相角,q=Vo/Vi.
通常,一个斩波周期T包含三个时段:S11和S22、导通,S12和S21关断的T1时段;S11和S22关断、S12和S21导通的T2时段;S11、S22、S12和S21都导通的T3时段。且有T1、T2、T3=T,m1+m2+m3=1,m1=m11=m22,m2=m12=m21。
“泵”式矩阵变换器的工作过程包含以下两步:
①在斩波周期T中的(T1+T2)时段,S0导通,等值线路如图2所标,分为两个独立回路:
回路a ,T1电流值上升,从电网吸收能量;
式中,ωi为输入频率,ωo为输出频率,ψ为输出初相角,q=Vo/Vi.
通常,一个斩波周期T包含三个时段:S11和S22、导通,S12和S21关断的T1时段;S11和S22关断、S12和S21导通的T2时段;S11、S22、S12和S21都导通的T3时段。且有T1、T2、T3=T,m1+m2+m3=1,m1=m11=m22,m2=m12=m21。
“泵”式矩阵变换器的工作过程包含以下两步:
①在斩波周期T中的(T1+T2)时段,S0导通,等值线路如图2所标,分为两个独立回路:
回路a ,T1电流值上升,从电网吸收能量;
 回路b--C1上的电压VC1(t)作为开关管矩阵的电源为负载提供能量。
在这段时间内,对开关矩阵而言又分为两个工作时段,即T1和T2。在T1时段内,S11和S22导通;在T2时段内,S21和S12导通。这里,根据T1/T2的变化,可以实现对波形的调制。
②在斩波周期T的T3时段,S0截止,等值电路如图3所示,同样也由两个独立回路构成:
回路a--L1释放能量,电源和L1趾联对C1充电,适当选择T3可使电容C1的充电电压VC1(t)大于电源电压,从而实现了"电压提升"。
回路b--S11、S12、S21、S22同时导通,可以等效为一个导通的SM,感性负载续流。
图3
要特别注意:此时开关矩阵并未直接与电源连接,因此S11、S12、S21和S22同时导通不会引起输入电源短路,感性负载通过它们提供的回路也不会出现过电压。
在泵式矩阵变换器的工作过程中,经过T3→(T1+T2)→T3的如此往复循环,通过L1和C1便将输入电压"泵升"到电容G1上的电压VC1(t),并作为开关矩阵的输入电源,提高了开关矩阵的输入电压;与此同时,开关矩阵经过T3→T1→T2→T3的斩波循环,也完成了"波形调制"。
1.3"泵式"矩阵变换器总电压传输比Q
回路b--C1上的电压VC1(t)作为开关管矩阵的电源为负载提供能量。
在这段时间内,对开关矩阵而言又分为两个工作时段,即T1和T2。在T1时段内,S11和S22导通;在T2时段内,S21和S12导通。这里,根据T1/T2的变化,可以实现对波形的调制。
②在斩波周期T的T3时段,S0截止,等值电路如图3所示,同样也由两个独立回路构成:
回路a--L1释放能量,电源和L1趾联对C1充电,适当选择T3可使电容C1的充电电压VC1(t)大于电源电压,从而实现了"电压提升"。
回路b--S11、S12、S21、S22同时导通,可以等效为一个导通的SM,感性负载续流。
图3
要特别注意:此时开关矩阵并未直接与电源连接,因此S11、S12、S21和S22同时导通不会引起输入电源短路,感性负载通过它们提供的回路也不会出现过电压。
在泵式矩阵变换器的工作过程中,经过T3→(T1+T2)→T3的如此往复循环,通过L1和C1便将输入电压"泵升"到电容G1上的电压VC1(t),并作为开关矩阵的输入电源,提高了开关矩阵的输入电压;与此同时,开关矩阵经过T3→T1→T2→T3的斩波循环,也完成了"波形调制"。
1.3"泵式"矩阵变换器总电压传输比Q
 (1)升压过程
开关管S0、电感L1、电容C1组成升压回路,其等效电路如图4所示。当S0导通时,L1从V1(t)电源吸收并储存能量;当S0截止,SM导通时,电源V1(t)与L1上的电势串联,向C1充电,这时可以认为C1是升压回路的负载,此后C1两端的电压便是开关矩阵的输入电压。
升压过程的电压传输比为[5]:
(2)降压过程
电容C1、C2与电感L2以及负载组成降压回路,其等效电路如图5所示。当S0闭合时,VC1(t)成为降压部分的输入电压,电容C1向负载和储能电感L2放电使L2储能;当开关管件S0截止且SM导通时,L2向负载释放能量(续流)。
降压过程的电压传输比为[5]:g2=m1+m2
(3)"泵式电路"电压传输比
显然,“泵”式电路的电压传输比为:
由公式(8)可知:当m3<0.5时,q0>1,Vc2(t)>V1(t),"泵"式电路将工作在升压状态。
(1)升压过程
开关管S0、电感L1、电容C1组成升压回路,其等效电路如图4所示。当S0导通时,L1从V1(t)电源吸收并储存能量;当S0截止,SM导通时,电源V1(t)与L1上的电势串联,向C1充电,这时可以认为C1是升压回路的负载,此后C1两端的电压便是开关矩阵的输入电压。
升压过程的电压传输比为[5]:
(2)降压过程
电容C1、C2与电感L2以及负载组成降压回路,其等效电路如图5所示。当S0闭合时,VC1(t)成为降压部分的输入电压,电容C1向负载和储能电感L2放电使L2储能;当开关管件S0截止且SM导通时,L2向负载释放能量(续流)。
降压过程的电压传输比为[5]:g2=m1+m2
(3)"泵式电路"电压传输比
显然,“泵”式电路的电压传输比为:
由公式(8)可知:当m3<0.5时,q0>1,Vc2(t)>V1(t),"泵"式电路将工作在升压状态。
 (4)开关矩阵斩波的电压传输比q
开关矩阵工作于波形调制方式时,开关矩阵具有输入/输出电压传输比q,在实时计算调制函数时,q是人为设定的。
(5)"泵"式矩阵变换器的电源输入/矩阵输出的总电压传输比Q
“泵”式矩阵变换器的总电压传输比为“泵电路”电压传输比和“波形调制”电压传输比之积:
当斩波周期T足够小时,在相邻的几个斩波周期中,可以认为m1、m2分别为常数。而在矩阵变换器工作中,m3为预先设定的常数。通过适当选择m3和q,可使Q>1。
图6
2 "泵式"矩阵变换器的仿真实验
为验证“泵式”矩阵变换器的拓扑结构与调制策略,采用Matlab/Simulink仿真软件建立仿真模型。仿真模型包括主电路和控制电路两部分。
图6给出了在负载电阻为22Ω,负载电感为10mH,q=0.5,m3=0.7,斩波频率为10kHz,输入峰值电压为100V,频率为50Hz,输出频率为75Hz、40Hz时,"泵"式矩阵变换器的输出电压波形。从图中可以看出电压传输比均大于1。
在仿真模型中设定不同电压传输比,以验证“泵”式矩阵变换器的理论和电压传输比的相关公式。在表1中列出了幅值为100V的输入电压,经"泵"式矩阵变换器的调制后的输出电压幅值与m3、q、Q的对应关系。
表1 “泵”式矩阵变换器输入/输出比(此时输入电压幅值为100V)
q
m3
Q
仿真输出电压幅值/V
0.1
0.1
0.9
95
0.7
0.3
33
0.3
0.1
2.7
288
0.7
0.9
93
结果表明:电压传输比可以双向调节;理论计算的总传输比Q与实测结果吻合。
针对矩阵变换器的电压传输比偏低的普遍性难题,本文以单相矩阵变换器为平台,突破经典矩阵变换器的约束条件和拓扑结构,提出了一种可以实现双向调节输出电压的“泵”式矩阵变换器,其电压传输比可大于1。
在详细分析了工作过程的基础上,给出了总控制电压传输比Q的计算公式。通过Matlab/Simulink软件的仿真模型,得到多组实验数据,验证了"泵"式矩阵变换器的调制策略和有关电压传输比的分析和计算公式,获得了期望的结果。
(4)开关矩阵斩波的电压传输比q
开关矩阵工作于波形调制方式时,开关矩阵具有输入/输出电压传输比q,在实时计算调制函数时,q是人为设定的。
(5)"泵"式矩阵变换器的电源输入/矩阵输出的总电压传输比Q
“泵”式矩阵变换器的总电压传输比为“泵电路”电压传输比和“波形调制”电压传输比之积:
当斩波周期T足够小时,在相邻的几个斩波周期中,可以认为m1、m2分别为常数。而在矩阵变换器工作中,m3为预先设定的常数。通过适当选择m3和q,可使Q>1。
图6
2 "泵式"矩阵变换器的仿真实验
为验证“泵式”矩阵变换器的拓扑结构与调制策略,采用Matlab/Simulink仿真软件建立仿真模型。仿真模型包括主电路和控制电路两部分。
图6给出了在负载电阻为22Ω,负载电感为10mH,q=0.5,m3=0.7,斩波频率为10kHz,输入峰值电压为100V,频率为50Hz,输出频率为75Hz、40Hz时,"泵"式矩阵变换器的输出电压波形。从图中可以看出电压传输比均大于1。
在仿真模型中设定不同电压传输比,以验证“泵”式矩阵变换器的理论和电压传输比的相关公式。在表1中列出了幅值为100V的输入电压,经"泵"式矩阵变换器的调制后的输出电压幅值与m3、q、Q的对应关系。
表1 “泵”式矩阵变换器输入/输出比(此时输入电压幅值为100V)
q
m3
Q
仿真输出电压幅值/V
0.1
0.1
0.9
95
0.7
0.3
33
0.3
0.1
2.7
288
0.7
0.9
93
结果表明:电压传输比可以双向调节;理论计算的总传输比Q与实测结果吻合。
针对矩阵变换器的电压传输比偏低的普遍性难题,本文以单相矩阵变换器为平台,突破经典矩阵变换器的约束条件和拓扑结构,提出了一种可以实现双向调节输出电压的“泵”式矩阵变换器,其电压传输比可大于1。
在详细分析了工作过程的基础上,给出了总控制电压传输比Q的计算公式。通过Matlab/Simulink软件的仿真模型,得到多组实验数据,验证了"泵"式矩阵变换器的调制策略和有关电压传输比的分析和计算公式,获得了期望的结果。 
 零基础学电子与Arduino:给编程新手的开发板入门指南
零基础学电子与Arduino:给编程新手的开发板入门指南 LM4250H/883B
LM4250H/883B










 京公网安备 11010802033920号
京公网安备 11010802033920号