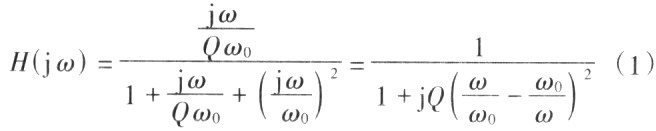 式中:ωo=2πfo,是中心角频率,fo是中心频率;Q是品质因数。
当ω=ωo时,H(iωo)=1。这说明带通滤波器在中心角频率ωo处的幅值尤衰减,相位无延时,这是带通滤波器的重要特性。这一特性保证了基于带通滤波器的谐波检测方法的准确性。
在有源滤波器里我们选择带通滤波器的中心频率fo为50Hz,则带通滤波器对基波幅疽无衰减,相位无延时,其它次谐波均被滤除,这就能实时地检测出基波。负载电流ia、ib、ic通过带通滤波器得到三相的基波电流ia1、ib1、ic1,用负载电流减去基波电流即可得到三相的谐波电流iah、ibh、ich。据此,谐波电流检测原理如图1所示。这种检测方法不需要坐标变换,只需要对三相电流分别进行带通滤波,大大减少了计算量。
式中:ωo=2πfo,是中心角频率,fo是中心频率;Q是品质因数。
当ω=ωo时,H(iωo)=1。这说明带通滤波器在中心角频率ωo处的幅值尤衰减,相位无延时,这是带通滤波器的重要特性。这一特性保证了基于带通滤波器的谐波检测方法的准确性。
在有源滤波器里我们选择带通滤波器的中心频率fo为50Hz,则带通滤波器对基波幅疽无衰减,相位无延时,其它次谐波均被滤除,这就能实时地检测出基波。负载电流ia、ib、ic通过带通滤波器得到三相的基波电流ia1、ib1、ic1,用负载电流减去基波电流即可得到三相的谐波电流iah、ibh、ich。据此,谐波电流检测原理如图1所示。这种检测方法不需要坐标变换,只需要对三相电流分别进行带通滤波,大大减少了计算量。
 3 数字带通滤波器的设计与实现
数字滤波器根据其类型可以分为IIR型和FIR型。PIR型只有零点,不容易像IIR型那样取得比较好的通带与阻带特性.所以,在一般的设计中选用IIR型。IlR型又可以分成Butterworth型滤波器,Chebyshev I型滤波器,Chcbyshev Ⅱ型滤波器和椭圆型滤波器等。MATLAB工具箱里面的数字滤波器设计工具FDATool可以帮助大家方便地选择和设计所需要的数字滤波器。
数字带通滤波器的主要参数包括阶数、滤波器类型、两个截止频率等。高阶滤波器的阻带衰减特性很好,但是,阶数高了之后难以实现。而对于有源滤波器来说,基波和主要谐波的频率相隔比较大,所以对阻带衰减率的要求不是很高,选用2阶滤波器就可以满足条件;又因为Buttermorth滤波器在通带内特性较平,而且实现起来比较简单,经综合考虑后,选用2阶Butterworth带通滤波器。
滤波器截止频率的选取和品质因数Q密切相关。Q越大,对谐波衰减越快,经带通滤波器提取出的基波分量越精确;但是,Q越大,带宽越小,动态响应速度会越慢,还会使数字滤波器的参数相差倍数过大,将增高对字长的要求。带通滤波器的通带宽度BW=ωo/(2πQ)=fo/Qofo是系统的中心频率。这里我们Q取在5左右,使得带宽大概在10Hz左右。选取两个截止频率分别为45Hz和55.6Hz。这里要注意的是。由于带通滤波器的幅频特性的不对称性,中心频率并不是两个截止频率的平均值。两个截止频率的选取标准是保证50Hz中心频率的相移为O并且幅值没有衰减。根据上面的标准设计出滤波器传递函数为
3 数字带通滤波器的设计与实现
数字滤波器根据其类型可以分为IIR型和FIR型。PIR型只有零点,不容易像IIR型那样取得比较好的通带与阻带特性.所以,在一般的设计中选用IIR型。IlR型又可以分成Butterworth型滤波器,Chebyshev I型滤波器,Chcbyshev Ⅱ型滤波器和椭圆型滤波器等。MATLAB工具箱里面的数字滤波器设计工具FDATool可以帮助大家方便地选择和设计所需要的数字滤波器。
数字带通滤波器的主要参数包括阶数、滤波器类型、两个截止频率等。高阶滤波器的阻带衰减特性很好,但是,阶数高了之后难以实现。而对于有源滤波器来说,基波和主要谐波的频率相隔比较大,所以对阻带衰减率的要求不是很高,选用2阶滤波器就可以满足条件;又因为Buttermorth滤波器在通带内特性较平,而且实现起来比较简单,经综合考虑后,选用2阶Butterworth带通滤波器。
滤波器截止频率的选取和品质因数Q密切相关。Q越大,对谐波衰减越快,经带通滤波器提取出的基波分量越精确;但是,Q越大,带宽越小,动态响应速度会越慢,还会使数字滤波器的参数相差倍数过大,将增高对字长的要求。带通滤波器的通带宽度BW=ωo/(2πQ)=fo/Qofo是系统的中心频率。这里我们Q取在5左右,使得带宽大概在10Hz左右。选取两个截止频率分别为45Hz和55.6Hz。这里要注意的是。由于带通滤波器的幅频特性的不对称性,中心频率并不是两个截止频率的平均值。两个截止频率的选取标准是保证50Hz中心频率的相移为O并且幅值没有衰减。根据上面的标准设计出滤波器传递函数为
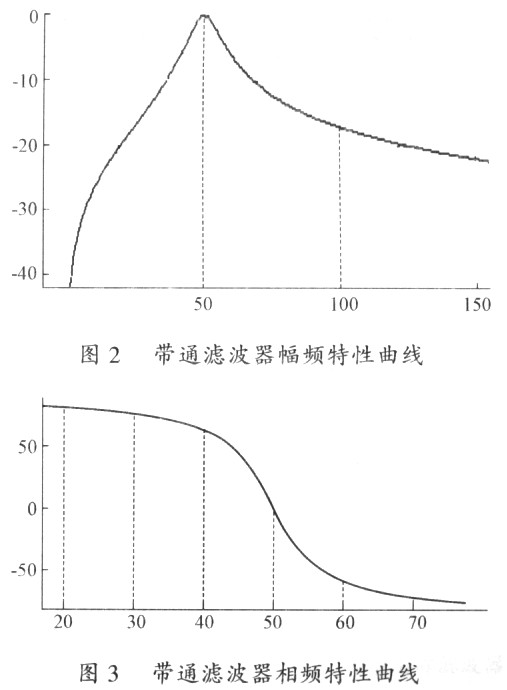
 滤波器的幅频和相频特性如图2及图3所示。
滤波器的幅频和相频特性如图2及图3所示。
 带通滤波器的实现就是在DSP芯片中实现式(2)的传递函数,为了便于程序实现,将式(2)改成差分方程的形式,如式(3)所示。
y(n)=0.003319x(n)-0.003319x(n-2)+1.9924y(n-1)-O.9934y(n-2) (3)
用DSP实现上面的差分方程主要是用3个存储器单元来保存x(n),x(n-1),x(n-2)的值,3个存储单元存储y(n),y(n-1),y(n-2)的值,在每一次中断程序中根据式(3)更新这6个存储单元的数值,最后输出的y(n)就是滤波之后的基波数值。如果采用其他形式的滤波器所需要的中间存储单元的数目可能是不一样的,要根据差分方程里面x(n)和y(n)的项数来确定。
如果带通滤波器程序是在定点DSP实现的话,还要注意滤波器系数的小数点位置选择。数字滤波器系数对滤波器性能影响非常大,一旦滤波器参数相差哪怕是很小一点,滤波器的输出就可能和正确数值相差很远,有时候还可能会使得系统不稳定,所以,应该尽量把系数放大之后冉计箅。这里我们根据3个系数(0.003319,1.9924,O.9934)和DSP(16位定点)的特点,把所有的系数都放大214倍,滤波运算结束之后再缩小214倍,使汁算的结果尽量准确。在滤波器实现中要根据滤波器系数来选择适当的放大倍数,原则就是尽量用满处理器的位数(这里就是16位),这一点非常重要。
4 系统仿真和试验结果
实验系统为三相并联型有源滤波器。检测部分的框图如图4所示,其中虚线部分是直流侧电压控制部分。系统的原理是:首先,负载电流通过带通滤波器之后得到基波电流ia1、ib1、ic1;然后,叠加上维持直流侧电压所需要的有功电流△iap、△ibp、△icp,再从总的负载电流中减去这部分电流,得到的就是三相指令电流值;最后,对指令电流值进行PI调节控制逆变器的输出,将谐波电流反相注入电网,使得电网的电流基本为正弦波。
带通滤波器的实现就是在DSP芯片中实现式(2)的传递函数,为了便于程序实现,将式(2)改成差分方程的形式,如式(3)所示。
y(n)=0.003319x(n)-0.003319x(n-2)+1.9924y(n-1)-O.9934y(n-2) (3)
用DSP实现上面的差分方程主要是用3个存储器单元来保存x(n),x(n-1),x(n-2)的值,3个存储单元存储y(n),y(n-1),y(n-2)的值,在每一次中断程序中根据式(3)更新这6个存储单元的数值,最后输出的y(n)就是滤波之后的基波数值。如果采用其他形式的滤波器所需要的中间存储单元的数目可能是不一样的,要根据差分方程里面x(n)和y(n)的项数来确定。
如果带通滤波器程序是在定点DSP实现的话,还要注意滤波器系数的小数点位置选择。数字滤波器系数对滤波器性能影响非常大,一旦滤波器参数相差哪怕是很小一点,滤波器的输出就可能和正确数值相差很远,有时候还可能会使得系统不稳定,所以,应该尽量把系数放大之后冉计箅。这里我们根据3个系数(0.003319,1.9924,O.9934)和DSP(16位定点)的特点,把所有的系数都放大214倍,滤波运算结束之后再缩小214倍,使汁算的结果尽量准确。在滤波器实现中要根据滤波器系数来选择适当的放大倍数,原则就是尽量用满处理器的位数(这里就是16位),这一点非常重要。
4 系统仿真和试验结果
实验系统为三相并联型有源滤波器。检测部分的框图如图4所示,其中虚线部分是直流侧电压控制部分。系统的原理是:首先,负载电流通过带通滤波器之后得到基波电流ia1、ib1、ic1;然后,叠加上维持直流侧电压所需要的有功电流△iap、△ibp、△icp,再从总的负载电流中减去这部分电流,得到的就是三相指令电流值;最后,对指令电流值进行PI调节控制逆变器的输出,将谐波电流反相注入电网,使得电网的电流基本为正弦波。
 系统仿真采用MATLAB里面的Simulink模块,仿真的结果如图5所示。从图5可以看出,补偿之后的电网电流比补偿以前的电流波形大大改善。
系统仿真采用MATLAB里面的Simulink模块,仿真的结果如图5所示。从图5可以看出,补偿之后的电网电流比补偿以前的电流波形大大改善。
 实验样机容量设计为6kW,输入电压为三相380V,负载为三相不控整流桥.控制部分以TI公司的TMS320LF2407 DSP为核心,负责谐波电流计算和PWM输出控制。
程序主要部分是在AD采样中断里面完成的,在AO中断程序里,首先根据三相的电压和电流采样数值,利用式(3)计算出滤波以后的电流,再汁算出指令电流值,最后通过PI调节之后送给PWM发生电路,控制逆变器的输出。
图6是程序的中间计算结果,图中1为DSP采样的电网电压,2为DSP采样的负载电流,3是负载电流通过带通滤波器得到的基波分量,从图6中可以看出,带通滤波器可以很好地分离出负载电流的基波分量。
实验样机容量设计为6kW,输入电压为三相380V,负载为三相不控整流桥.控制部分以TI公司的TMS320LF2407 DSP为核心,负责谐波电流计算和PWM输出控制。
程序主要部分是在AD采样中断里面完成的,在AO中断程序里,首先根据三相的电压和电流采样数值,利用式(3)计算出滤波以后的电流,再汁算出指令电流值,最后通过PI调节之后送给PWM发生电路,控制逆变器的输出。
图6是程序的中间计算结果,图中1为DSP采样的电网电压,2为DSP采样的负载电流,3是负载电流通过带通滤波器得到的基波分量,从图6中可以看出,带通滤波器可以很好地分离出负载电流的基波分量。
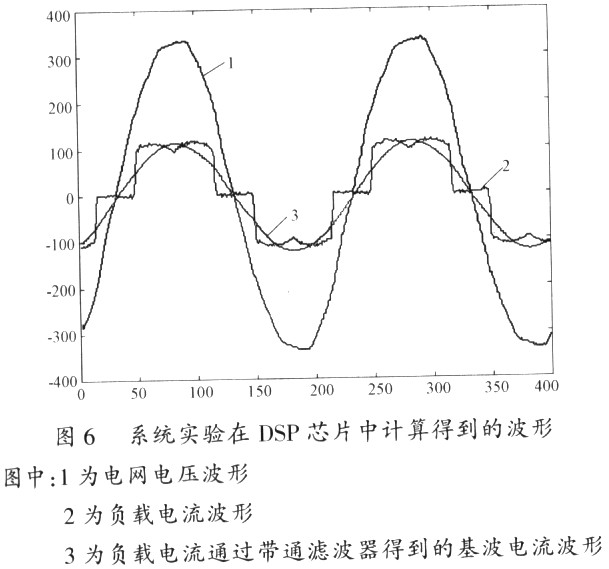 图7为系统的实验波形,其中图7(a)为有源滤波器投入前的电网电压和电流波形,图7(b)是有源滤波器投入后的电网电压和电流波形,从图7(b)可以看出,基于带通滤波器的有源滤波器能起到很好的谐波抑制作用。
图7为系统的实验波形,其中图7(a)为有源滤波器投入前的电网电压和电流波形,图7(b)是有源滤波器投入后的电网电压和电流波形,从图7(b)可以看出,基于带通滤波器的有源滤波器能起到很好的谐波抑制作用。
 5 结语
本文提出了一种基于带通滤波器的谐波检测方法,并通过仿真和实验验证了这种方法在并联型有源滤波器中应用的可行性。得到的主要结论如下:
1)利用带通滤波器可以比较好地检测出负载电流中的基波分量;
2)由于滤波器负载电流一般没有偶次谐波,如果是三相对称系统也没有3次以及3的倍数次谐波,所以,只要带通滤波器的中心频率是50Hz,带宽对系统的影响不是很大,但是,带通滤波器的相频特性对系统的影响比较大;
3)试验证明基于带通滤波器的并联型有源滤波器可以有效抑制电网的谐波电流,但是,这种方法的缺点是它不能同时补偿无功功率。
5 结语
本文提出了一种基于带通滤波器的谐波检测方法,并通过仿真和实验验证了这种方法在并联型有源滤波器中应用的可行性。得到的主要结论如下:
1)利用带通滤波器可以比较好地检测出负载电流中的基波分量;
2)由于滤波器负载电流一般没有偶次谐波,如果是三相对称系统也没有3次以及3的倍数次谐波,所以,只要带通滤波器的中心频率是50Hz,带宽对系统的影响不是很大,但是,带通滤波器的相频特性对系统的影响比较大;
3)试验证明基于带通滤波器的并联型有源滤波器可以有效抑制电网的谐波电流,但是,这种方法的缺点是它不能同时补偿无功功率。
上一篇:高精度锂电池监测芯片DS2762的原理及应用
下一篇:电动汽车电池管理系统的多路电压采集电路设计
- 热门资源推荐
- 热门放大器推荐

Vishay线上图书馆
- 选型-汽车级表面贴装和通孔超快整流器
- 你知道吗?DC-LINK电容在高湿条件下具有高度稳定性
- microBUCK和microBRICK直流/直流稳压器解决方案
- SOP-4小型封装光伏MOSFET驱动器VOMDA1271
- 使用薄膜、大功率、背接触式电阻的优势
- SQJQ140E车规级N沟道40V MOSFET

- Vishay推出适用于恶劣环境的紧凑型密封式SMD微调电阻器
- MathWorks 和 NXP 合作推出用于电池管理系统的 Model-Based Design Toolbox
- 意法半导体先进的电隔离栅极驱动器 STGAP3S为 IGBT 和 SiC MOSFET 提供灵活的保护功能
- 全新无隔膜固态锂电池技术问世:正负极距离小于0.000001米
- 东芝推出具有低导通电阻和高可靠性的适用于车载牵引逆变器的最新款1200 V SiC MOSFET
- 【“源”察秋毫系列】 下一代半导体氧化镓器件光电探测器应用与测试
- 采用自主设计封装,绝缘电阻显著提高!ROHM开发出更高电压xEV系统的SiC肖特基势垒二极管
- 艾迈斯欧司朗发布OSCONIQ® C 3030 LED:打造未来户外及体育场照明新标杆
- 氮化镓取代碳化硅?PI颠覆式1700V InnoMux2先来打个样
- Allegro MicroSystems 在 2024 年德国慕尼黑电子展上推出先进的磁性和电感式位置感测解决方案
- 左手车钥匙,右手活体检测雷达,UWB上车势在必行!
- 狂飙十年,国产CIS挤上牌桌
- 神盾短刀电池+雷神EM-i超级电混,吉利新能源甩出了两张“王炸”
- 浅谈功能安全之故障(fault),错误(error),失效(failure)
- 智能汽车2.0周期,这几大核心产业链迎来重大机会!
- 美日研发新型电池,宁德时代面临挑战?中国新能源电池产业如何应对?
- Rambus推出业界首款HBM 4控制器IP:背后有哪些技术细节?
- 村田推出高精度汽车用6轴惯性传感器
- 福特获得预充电报警专利 有助于节约成本和应对紧急情况

 SA58601D
SA58601D










 京公网安备 11010802033920号
京公网安备 11010802033920号