通过分析SKJ-II型数字随动系统中PWM装置的工作原理,建立了模型公式并推算出理论传递函数关系。根据模型公式得到了PWM装置系统化的理论传递函数,并通过实验验证了理论传递函数的正确性,并指出模型中电源电压需要考虑开关的管压降问题。对于应用PWM技术进行功率变换的控制系统的建模有理论指导意义。
1 引言
目前,直流PWM调速系统凭借开关频率高,低速运行稳定,动态性能优良等优点,应用日益广泛,特别是在中、小容量的高动态性能系统中。
PWM控制与变换器(简称PWM装置)是直流脉宽调速系统中的重要组成环节,而对于PWM装置的数学模型,文献中仅给出最后近似的传递函数,并未解释其中框图变换的过程和参数分析。SKJ-II型数字随动系统内部含有调速环,其中就包含PWM装置,这里基于该系统中使用的PWM装置模型进行拓展分析,以便获得其模型的推导及变换过程,为PWM装置模型提供必要的理论依据。
2 模型建立与框图分析
SKJ-II型数字随动系统的结构如图1所示。功率放大器环节起到PWM控制器和PWM变换器的作用。
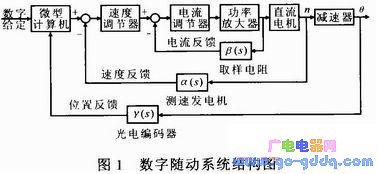
为了方便研究,将功率放大器环节内容分为两步,分别简称为PWM控制器和H桥,UX11(s)信号作为PWM装置的输入,Ud(s)为PWM装置的输出,ρ(s)为中间量。
2.1 静态分析
实现PWM控制器的电路如图2所示。预建立PWM装置的模型,先确定其输入信号,输入信号为UX11(X11端输入信号),该信号由系统前端的电流调节器的输出决定。图中,XJ7端为三角波发生电路的输出端,三角波发生电路中运算放大器A1:A构成加法器,运算放大器A1:B构成反向积分器,电位器P2主要用来控制产生的三角波的频率,2DW232是双向稳压二极管,起了限幅的作用。运算放大器A3:A以及外围电阻构成了一个反相加法放大电路,由于放大倍数较大,故小信号时才线性放大,大信号时会工作在非线性饱和状态。
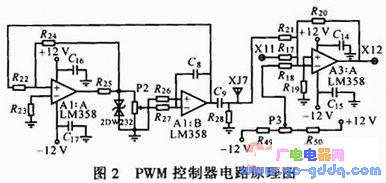
当X11端输入信号接地,即UX11=0 V时,利用GDS1102A数字示波器测量XJ7端和X12端的波形,分别记为uXJ7和uX12,两者波形如图3所示。
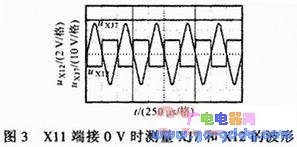
当uXJ7较小时,反相放大倍数为50;当uXJ7较大时,运算放大器A3:A会饱和,输出波形是正负对称的梯形波,但图中输出波形很接近矩形波,称该梯形波为近似矩形波,其占空比是50.81%。
PWM控制是对脉冲的宽度进行调制的技术,在此通过调制近似矩形波的占空比来实现PWM控制。当X11端输入电压信号,则近似矩形波占空比会产生相应改变。当运算放大器A3:A工作在线性状态,忽略调零通路作用,则流过R18电流为零,规定电流经R21,R20,R17一端流向R21,R20,R17的公共端为电流的正方向,并假设运放为理想运算放大器,根据KCL定理可得:
iR21+IR17+iR20=0 (1)
根据理想运算放大器的性质可知UA3_2=0 V,由欧姆定律可得:
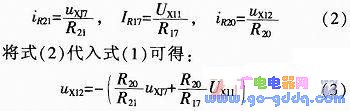
分析X11端输入UX11为零时情况,记X12端饱和输出电压为+U0。当uX12=-U0(即负饱和)时,代入式(3)可得:uXJ7=U0R21/R20;当uX12= U0(即正饱和)时,代入式(3)可得:uXJ7=-U0R21/R20。记XJ7端输出三角波的幅值范围为[-U1,U1],周期为T,则有X12端输出梯形波单个周期的线性放大时间t1、输出正饱和时间t2、输出负饱和时间t3为:
t1=(R21U0)T/(R20U1),t2=t3=0.5(T-t1) (4)
按照矩形波占空比的定义,则有PWM控制器输出矩形波的占空比为:
![]()
当然,实际输出波形并非理想的矩形波,而是梯形波,具体梯形波如何描述占空比暂且不讨论,假设各周期内线性区工作时间t1相对于这个周期的总时间T非常小,则可忽略其线性区时间t1,则X12端输出矩形波的占空比ρ=t2/(t2+t3)=0.5。
由上述推算可以得到结论:当输入UX11=0 V时,若uXJ7为正负对称的理想三角波,则运放器A3:A的反相端输入信号(R20/R21)uXJ7依然为正负对称的三角波。X12端占空比为50%,即输出负饱和时间与输出正饱和时间相等,实验测试结果如图3所示,示波器中显示占空比为50.81%,有1.62%的误差,除了示波器的测量误差还应注意此处计算占空比忽略了线性区时间t1。
2.2 动态分析
实际PWM控制器输入端是uX11,即电流控制器的输出,PWM控制器输出端是ρ,静态分析时uX11=0 V,输出ρ=0.5,动态工作时,ρ会随uX11变化而变化,取拉普拉斯变换,则输入记为UX11(s),输出记为ρ(s),中间信号记为UX12(s)和UXJ7(s),则式(3)可以改写为:
![]()
动态分析时,UXJ7仍然输入正负对称的三角波,但X11端输入UX11(s)不为零。
当UX11(s)>0时,由线性叠加定理可知,式(6)中R20UXJ7(s)/R21+R20UX11(s)/R17波形会上抬,成为正三角时间长而负三角时间短的正负不对称三角波,反相限幅后输出负饱和的时间比输出正饱和的时间长,即PWM控制器输出负饱和的时间比输出正饱和的时间长。当UX11(s)增大到正临界值UX11max时,刚好不出现线性区,更无正饱和,仅有负饱和,则满足:
综合式(9)和式(12)可得:若满足输入UX11(s)在[UX11max,UX11max范围内,则运放器A3:A以及外围电路构成的PWM控制器输出的占空比ρ(s)随着UX11(s)变化,超出该范围则ρ(s)饱和(即ρ要么为0,要么为1)。当UX12(s)=-U0(即负饱和)时,代入式(6)可推算此时XJ7端三角波信号满足:
若XJ7端三角波为理想的三角波,当UX11(s)>UX11max或UX11(s) SKJ-II型数字随动系统中使用了桥式可逆PWM变换器,其供电电源为Us,则输出电压Ud(s)与ρ(s)之间的关系为: Ud(s)=Us[2ρ(s)-1] (18) SKJ-II型数字随动系统元件参数:R17=22 kΩ,R20=20 kΩ,R21=1 MΩ,经示波器测量图4所示X12端饱和输出电压±11.6 V,三角波幅值范围为[-5.15 V,5.15 V],代入式(17)可得: ρ(s)=0.5-0.092 4UX11(s) (19) 通过等效变换,PWM装置的传递函数Ud(s)=-0.184 8UX11(s),相当于一个反向比例放大环节。 3 实验验证及公式修正 基于SKJ-II型数字随动系统,就PWM控制器电路和H桥电路的模型分别进行实验验证。实验中为降低难度不直接用力矩电机做实验,采用100 Ω滑线变阻器作为负载。输入信号UX11(s)由系统前端电流调节器的输出决定,H桥电路的输出Ud(s)为X16端与X17端之差,输出Ud(s)的占空比记为ρ(s)。测量X11端输入信号UX11(s)分别为1 V,2 V,3 V,-1 V,-2 V,-3 V时,输出X16端与X17端的波形数据,如表1所示。 ρ(s)修正参数定义为:△ρ=[1-ρ(s)测1-ρ(s)测2]/2,则修正后的占空比ρ(s)=ρ(s)测1+△ρ。一方面,假设GPWM(s)是PWM控制器传递函数,则: ρ(s)=0.5+GPWM(s)UX11(s) (20) 将上式变换可得:GPWM(s)=[ρ(s)-0.5]/UX11(s)。根据表1可得:当UX11(s)=1 V时,GPWM=-0.091 2;当UX11(s)=2 V时,GPWM=-0.092 5;当UX11(s)=3 V时,GPWM=-0.091 8;当UX11(s)=-1 V时,GPWM=-0.095 1;当UX11(s)=-2 V时,GPWM=-0.093 3;当UX11(s)= -3 V时,GPWM=-0.092 2。 另一方面,电源电压为Us时,Ud(s)=2Usρ(s)-Us。但实际上H桥还要考虑开关管的管压降,记△U为管压降。当电源电压为Us’时,则:Us=Us’-△U。那么,Ud(s)=2Usρ(s)-Us可以表示为: Ud(s)=[2ρ(s)-1](Us’-△U) (21) 由上式可得: △U=Us’-Ud(s)/[2ρ(s)-1] (22) 万用表测得Us’=22.9 V,根据表1的数据和式(22)可得:当Ux11(s)=1 V时,△U=0.147 8 V;当UX11(s)=2 V时,△U=0.419 6 V;当UX11(s)=3 V时,△U=0.312 3 V;当UX11(s)=-1 V时,△U=0.348 1 V;当UX11(s)=-2 V时,△U=0.451 7V;当UX11(s)=-3V时,△U=0.4 226V。 根据GPWM平均值得ρ(s)实验式为: ρ(s)测=0.5-0.092 7UX11(s) (23) 式(23)与式(19)比较,误差为0.325%。 根据△U的平均值可得Ud(s)实验公式为: Ud(s)测=[2ρ(s)-1](Us’-0.365 35) (24) 将式(24)与式(18)比较可得,实际的电源电压Us是考虑了开关管的管压降后的电源电压。将式(23)代入式(24),可得: Ud(s)测=-0.185 4UsUX11(s) (25) 其中,Us=Us’-0.365 35=22.534 6,将式(25)与Ud(s)=-0.184 8UX11(s)比较,误差为0.325%,与ρ(s)的误差一致。但是PWM装置的响应会有延迟,假设延迟时间为ts(t 4 结论 首先基于SKJ-II型数字随动系统,针对系统中的功率放大器环节,建立其数学模型,根据具体电路中的器件参数定量计算模型参数,确定具体的理论公式,并最终得到输入输出之间的传递函数关系式。清晰地分析证明了在一般的电力拖动自动控制系统中PWM装置可近似看成是一个带有纯滞后的比例环节。最后通过实验,进一步验证了理论推导的准确性。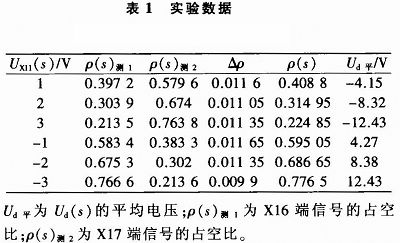

 机器人学 (蔡自兴)
机器人学 (蔡自兴) 零基础学电子与Arduino:给编程新手的开发板入门指南
零基础学电子与Arduino:给编程新手的开发板入门指南












 京公网安备 11010802033920号
京公网安备 11010802033920号