摘要:电荷泵式电子镇流器,采用充电电容和高频交流源,以实现功率因数校正(PFC),这已成为荧光灯镇流器中极有吸引力的电路拓扑。但这种电路还存在一些问题,如输入电流的THD值高,灯电流的波峰比(CF)高。对这些问题产生的根源进行了分析,并提出解决方法。附加两只小型箝位二极管后,在开环控制状态,就可使输入电流波形得到很好的改善,从而使PF>0.99,THD<5%,而灯电流的CF<1.6。并给出了实验结果。
关键词:电子镇流器;功率因数校正;电路
Analysis and Improvement for Charge Pump Electronic Ballast
GAO Ji-sun
Abstract:The charge pump electronic ballast circuit which employs a charging capacitor and a high frequency AC source to implement the power factor correction(PFC)has become an attractive topology for the ballast of the fluorescent lamp. But, this circuit has some problems, such as higher total harmonic distortion(THD)of the input current and higher crest factor(CF)of the lamp current. The origin of the problems is analyzed and asolution is proposed. With the addition of two small clamping diodes, very good input current(PF>0.99,THD<5%)and lamp current(CF<1.6)can be obtained with the open loop control. The experimental results are provided for verification.
Keywords:Electronic ballast;Power factor correction;Circuit
1 引言
普通电子镇流器拓扑,由带无源LC滤波器的桥式整流电路和高频逆变器组成,它已不能满足电网的严格要求,如线路输入端的功率因数要高,电网电流的THD要低等。断续升压式PWM变换器及其拓扑,可采用简单的控制电路,达到较高的功率因数,不过,它需要附加一只笨重的升压电感器,此外,开关功率管上的电压/电流应力一般也比较大。综合考虑,该电子镇流器的性能/价格比就不会太高。近年来,采用充电电容和高频交流源来进行功率因数校正(PFC)的电子镇流器成为极具吸引力的电路拓扑。因为,充电电容器按类似“电荷泵”的方式来调整输入电流的波形,这类电路,也叫做“电荷泵”功率调节器。因为在电路中,取消了升压电感器,输入端的LC滤波器的体积就大大减小了,镇流器的成本还可能降低。但是,其输入电流的THD>15%,灯电流的CF>2.4。本文在对该“电荷泵”电路的工作原理和存在问题进行分析后,采用二极管箝位技术克服了这些存在的问题,使在开环控制下,就能得到良好的输入电流和灯电流波形。为了验证理论分析结论,还提供了实验结果。
2 工作原理和存在问题
图1为典型的“电荷泵”式电子镇流器电路图,图中Lr与Cr是谐振元件,Cb1是隔直电容。该电路和普通镇流器电路的区别是:普通镇流器是在整流桥后紧接高频逆变器,而本电路是增加了一只电容Cin和二极管Dc,这两个元件在调整输入电流波形方面起到了关键作用。图1电路可分为两部分:PFC及DC/AC逆变。图2为其PFC部分的等效电路和理想波形。为了简化分析,把Cr两端的电压看作独立的高频电压源(Ua)。通过设计,使直流母线电压Udc高于输入的电网电压Ug,二极管Dc不会导通。从而,输入电流就等于Cin的的正向充电电流,电流的方向如图2(a)所示 。 这 是 通 过 调 节ug和udc来 实 现 的 。 如 果Cin上 电 荷 的 变 化 〔 它 正 比 于Cin两 端 电 压 的 变 化 , 即ucmax-ucmin。 参 看 图 2( b) 〕 紧 跟 着 输 入 电 压ug变 化 , 则 可 使 功 率 因 数 达 到 1。 具 体 分 析 如 下 :

(a) 阶段1 (b)阶段2 (c) 阶段3 (d) 阶段4
图1 典型电荷泵电子镇流器电路
图2 PFC原理
(a) 等效电路 (b) 理想的波形
2.1 PFC原理分析
在一个开关周期内电荷泵电路的稳态工作,可分为四个拓扑阶段,如图3所示。理论波形如图4所示。

图3 PFC电 路 的 四 个 拓 扑 阶 段

图4 PFC电 路 的 理 论 波 形
1)阶段1[0~α]
在这个阶段,因为节点B处的电压ub低于Udc,而高于ug,ug 在ω t=α,DB开始导通,ub被箝位到ug,使ub为恒定值。当ua继续下降时,uc必然增加。这样Cin被整流的电网电流充电。在ω t=π时,ua降至uamin,而uc则达到其最大值。
ucmax=ug-uamin (1)
3)阶段3[π~(π+β)]
在ω t=π之后,ua从uamin开始增加,ub变得大于ug,迫使DB关断,因为ub低于udc,二极管Dc仍被阻断。同阶段1类似,电容Cin中无电流通过,uc维持不变。ua继续增加,ub继续提升,在ω t=π+β时,此阶段结束。
4)阶段4[(π+β)~2π]
在ω t=π+β时,ub变得等于udc,二极管Dc开始导通,因为ub被箝位到udc,当ua继续增加时,uc必然下降。Cin的放电电流流入udc,在ω t=2π时,ua增加到uamax,而uc达到其最小值。
ucmin=ug-uamax (2)
在ω t=2π时,该电路工作又进入阶段1,重复下一个开关周期。
从上面分析可以看出,在该电路中的输入电流是断续的,它只在阶段2内有电流流过。在此阶段内,Cin上的电荷变化是:
ΔQch=Cin(ucmax-ucmin) (3)
把式(1)和式(2)代入式(3),并考虑到在阶段2时
udc=ug可得到
ΔQch=Cin(ug+2Up-udc) (4)
式中:2Up=uamax-uamin——ua的交流峰-峰值。
因为,在整个开关周期内,整流二极管只在阶段2内导通,则一个周期内的平均输入电流就等于Cin的平均充电电流,即:
iin,av=fsΔQch=fsCin(ug+2Up-udc) (5)
要使功率因数值大,就期望输入电流紧紧跟随输入电压,即:
iin,av∝ug (6)
如果在设计时,使
udc=2Up=ua,max-ua,min (7)
就会有:
iin,av=fsCinug∝ug (8)
这就意味着,如果满足式(7),该电路就会有良好的功率因数。这里,假定ua是正弦波形。事实上,ua可能是幅值恒定的其它任何波形。ua的直流偏置,也不是决定输入电流波形的因素。只要ua的峰-峰值(2Up)等于udc,就能保证获得良好的功率因数。
从式(5)还可看出,2Up不应小于udc,这可避免电网电压过零时,电网电流发生波形畸变。如果2Up 在实际电路中,输入电流可能畸变。这是由于Cin对逆变器电路的影响。该逆变器的工作可分为三个等效的拓扑,如图5所示。图5中R1a'是灯的等效电阻。图5表明,电容Cin在阶段1及阶段3,并不影响电路工作,但在阶段2和阶段4,Cin被接入了谐振电路。在交流等效电路中,Cin同Cr并联起来了。因此,该等效的逆变器,可近似为图6的电路。等效谐振电容值等于Cineq+Cr(而Cb1仅仅是个隔直电容)。
图5 逆 变 器 工 作 的 三 个 子 拓 扑
转换后Cin的等效值可近似为一个可变电容Cineq,如图6所示。因为,在一个开关周期内,由Cineq泵入谐振电路中的电荷可由式(4)表示,Cineq两端上的电压变化等于2Up,则该等效的输入电容可以这样估算:
Cineq=ΔQch/ΔU=Cin(ug+2Up-udc)/2Up (9)
通常,在交流电网电压半周期内,2Up和udc的变化是很小的,可通过适当的设计,使udc≈2Up,总能保持住。所以式(9)可写成
Cineq≌Cin(ug/2Up)∝ug (10)
尽管式(10)从数学上讲不是严密的。但它使我们能较好地理解Cin对谐振电路的影响。一般地说,由于Cin的影响,总的谐振电容值(Cr+Cineq)是随着电网电压ug的下降而减小,如式(10)所示。这使得高频交流电压ua的幅值在电网电压半周期内成为可变的。从而,在此半周期内,式(7)就不能成立。于是,输入电流波形畸变了,THD也升高了。因为,灯的阻抗很接近一个具有负的动态值的电阻(负阻),则灯管电压上叠加的100Hz的纹波也会在灯电流波形上引发较强的100Hz纹波。结果,灯电流的波峰比CF值也变高了。
当电网电压变低时,总的谐振电容就变小了。在轻载状态,这可能引起该逆变器的谐振频率偏移到高于开关频率,谐振电路的电流iL将会超前回路电压ut。结果,导致功率开关管MOSFET不能在零电压下开 关 (ZVS) ( 详 见3中 的 论 述 ) 。 在 高 频 工 作 时 ,MOSFET中 的 二 极 管 的 反 向 恢 复 电 流 可 能 会 损 坏MOSFET器 件 ( 详 见3中 的 例 子 ) 。
虽然,选用大的Cr(Cr》Cin)可能会降低Cin引起的影响,但谐振电感器中的电流应力仍然很高。所以,从效率和Lr的体积尺寸两者来考虑,选用大的Cr并不可取。
3 改善输入电流及灯电流波形的办法
根据式(5),要获得正弦输入电流波形,有两个途径:一是调整MOSFET管的开关频率fs,二是获得一种关系式:2Up=udc。调整fs就需要复杂的控制电路,况且,也难保证得到低的灯电流波峰比CF。因此,设法使2Up=udc,是可选择的途径。
3.1 基本的解决思路
图1基本电路的波形示于图7。由于Cin的调制作用,ua的包络线上有明显的100Hz纹波。uc的变化,也不能跟随输入电压ug。为得到良好的输入功率因数,应该滤平ua的包络。在特殊情况下,2Up总是大于udc,可以采用二极管箝位技术,来滤平ua的包络。此电路示于图8,其波形如图9所示。ua的包络被箝在udc(在这种情况下,uamax=udc,uamin=0),式(7)总能成立。可获得正弦输入电流波形。
图 7 基 本 电 荷 泵 电 路 中 的ua及uc波 形 (2Up>udc)
(c) 模 态3:iL> 0,ua=udc
(d) 模 态4:iL>0,0 (e) 模 态5:iL< 0,0
3.2 工作原理
该逆变电路的稳态工作可分成六个工作模态,如图10所示。图中,ZA代表Cineg,Cr及R1a'+Cb1的等效组合。图11为该电路的仿真波形。在下面讨论中,正向电流和电压的方向按图10所示定义。
1)模态1
S2关断,电感电流反向流经D1,使S1可在ZVS状态导通。在这种模态下,ua小于udc,uLr1总是正的。从而,电感电流iL的幅值下降,当iL降到零时,这种模态结束。
2)模态2
S1导通,因为ua处于0和udc之间,Da1和Da2均截止。由于电感电压的极性关系,电感电流iL维持正向增长。当ua达到udc时,这个模态结束。
3)模态3(箝位模态或续流阶段)
Da1导通,ua被箝位到udc,uLr1为零。因此iL通过Da1和S1续流。当S1截止时,该模态结束。
4)模态4
S1截止,迫使正向的电感电流流经D2。从而使S2以ZVS导通。在这种工作模态中,ua总是正的,所以,电感电压uLr1总是负的,电感电流的幅值下降。当电感电流变成零时,该模态结束。
5)模态5
S2导通,Da1和Da2都不导通。因为ua是处在udc和零之间。加在Lr1上的电压是负的。因此,电感电流按反方向增加,如图11所示。在降到零时,该模态结束。
(uf为 开 关 电 压 , 虚 线 为 无 箝 位 二 极 管 , 实 线 为 有 箝 位 二 极 管 )
6)模态6(箝位模态或续流阶段)
Da2导通,ua被箝位到零。电感电流经过Da2及S2续流。在S2截止时,该模态结束,又接着模态1开始下一个循环。
图11表明了有箝位二极管和没有箝位二极管的波形图。没有箝位二极管时,谐振电路电流超前回路电压,不能保证ZVS状态。但是在有箝位二极管时,谐振电路电流就变得滞后回路电压了(由于被箝位二极管引发的续流阶段),MOSFET中的二极管在该开关管导通前总是导通着。自然就可得到ZVS状态。所以,在采用了二极管箝位技术后,ZVS的负载范围变宽了。通过适当的设计,使该箝位二极管只在很短时间内导通,这样箝位二极管的电流应力就会很小。
3.3 进一步的改进措施
从图11可看出,图8所示电路中的灯电压波形(ua-udc/2)不是正弦波,这是由于箝位工作模态所致,从而,灯电流中就存在高频谐波分量。这会引起EM1辐射问题。此外,在负载变轻时,该基本电路会受较高的电压应力。这可采用第二级谐振技术来解决。图12为最后所形成的电路。图中Lr2和Cr2构成第二级谐振电路。这可以在负载变轻时,把直流母线上的电压降低,并且还提供必要的电压变换增益去点亮灯管,同时又满足式(7)(这是高功率因数所需要的),由于Lr2及Cr2的低通滤波作用,灯电流波形就接近正弦波。其EM1辐射就小了。因为ua的包络线被箝到udc,灯电流中电网频率的纹波也会很小,灯电流的波峰比也下降了。
4 实验结果
为验证上面的理论分析,进行了实验。图13是在图12中没有箝位二极管时的波形。其功率因数为98%,而输入电流的THD是10.4%,灯电流的波峰比CF是2.4。
图14是有箝位二极管时的波形(电路参见图12)。图中元件参数如下:Lr1=400μH,Cr1=1.2nF,Cin=28nF,Lr2=800μH,Cr2=9.4nF;输入电网电压是交流220V,所以udc为310V,工作频率为50kHz。功率因数0.995,THD是4.5%,CF是1.58。
图12电路同图1所示的基本电路相比较,所用磁性元件数相同。图1所示电路中的变压器是必不可少的,这是为了获得适当的电压变比,去点亮灯管,同时要满足式(7)。但图1电路中的谐振电感器的体积尺寸很大,因为它必须在灯点亮瞬间,能维持较大的伏·秒积(在灯点亮瞬间,灯电流较大,有大的电流通过谐振电感,此时,电感不应进入磁饱和)。相反,谐振电感器的Lr1体积尺寸却小得多,因为,在点灯瞬间,Lr2和Cr2之间的第二次谐振,使得ua很小。实验结果表明,所用磁材总体积从基本电路中62cm3降到新电路中的42cm3。虽然在新电路中多用了2只二极管,但新电路中,整个半导体开关器件上的电压应力却大大低于基本电路的电压应力。因而,开关器件的价格也降低了。 5 结语
基本的“电荷泵”电子镇流器电路,输入电流的THD高,灯电流的CF高,此外,在轻负载时和低的电网电压时,不易保持ZVS状态。而通过采用简单的二极管箝位技术,使输入电流的波形和灯电流的波形大大改善了,THD和CF明显地降低了。而由于引入了续流阶段,使ZVS也容易维持。此外,由于磁性元件体积的减小,半导体开关管上电压应力的减小,使新电路的成本也降低了。 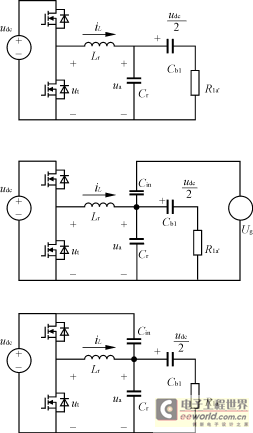
(a) 阶 段1,3 (b) 阶 段2 (c) 阶 段4

图 6 近 似 等 效 的 逆 变 器

(a) ua波 形 (b) uc波 形

图8 带 箝 位 二 极 管 后 的 改 进 电 路

(a) 模 态1:iL< 0,0?ua
图 10 在 新 电 路 中 的 六 个 工 作 模 态

图11 新 电 路 的 理 论 波 形 图

图12 采 用 二 级 谐 振 有 箝 位 二 极 管 的 镇 流 器 电 路

图 13 没 有 箝 位 二 极 管 时 的 波 形

图14 采 用 二 级 谐 振 有 箝 位 二 极 管 时 的 波 形
上一篇:PWM斩波器式交流稳压电源的原理分析
下一篇:单周控制DC/DC变换器的交流小信号模型与设计
- 热门资源推荐
- 热门放大器推荐

 Verilog HDL数字集成电路设计原理与应用
Verilog HDL数字集成电路设计原理与应用 8102302HA
8102302HA










 京公网安备 11010802033920号
京公网安备 11010802033920号