| 从前面叙述可知,如果一个线性控制系统是稳定的,那么从任何初始条件开始,经过一段时间就可以认为它的过渡过程已经结束,进入与初始条件无关而仅由外作用决定的状态,即稳态。控制系统在稳态下的精度如何,这是它的一个重要的技术指标,通常用稳态下输出量的要求值与实际值之间的差来衡量。如果这个差是常数,则称为稳态误差。
控制系统的稳态误差是因输入信号不同而不同的。因此就需要规定一些典型输入信号。通过评价系统在这些典型输入信号作用下的稳态误差来衡量和比较系统的稳态性能。在控制工程中通常采用的典型输入信号有以下几种:
1.单位阶跃函数:
其拉普拉斯变换为R(s)=1/s。
2.单位斜坡函数
其拉普拉斯变换为R(s)=1/s2。
3.单位加速度函数:
其拉普拉斯变换为R(s)=1/s3。
4.单位脉冲函数
其拉普拉斯变换为R(s)=1。
5.正弦函数:
其中最常用的典型信号为单位阶跃、单位斜坡、单位加速度三种输入信号。 3.2.2稳态误差和误差传递函数
系统的稳态误差是指系统在稳定状态下其实际输出值(在实际工作中常用系统输出的测量值代替)与给定值之差。对稳定的单输入单输出系统,稳态误差是时域中衡量系统稳态响应的性能指标,它反映了系统的稳态精度,因此稳态误差分析是控制系统分析的一项基本内容。
设有如图3-1所示的系统。它的闭环传函为
误差信号e(t)和输入信号r(t)之间的传递函数是
其中误差e(t)是输入信号和反馈信号之差。
 |
| |
| 图3-1控制系统 |
终值定理为求稳定系统的稳态误差提供了一个简便的方法。因为E(s)是
则稳态误差是
3.2.3 静态误差系数
当系统的输入信号为单位阶跃、单位斜坡和单位加速度三种典型信号之一时,上式分别化为:
单输入单输出线性系统的传递函数一般表示为:
单位阶跃函数:
 |
(3-2) |
单位斜坡函数:
 |
(3-3) |
单位加速度函数:
 |
(3-4) |
现定义误差系数如下:
静态位置误差系数Kp:
 |
(3-5) |
静态速度误差系数Kv:
 |
(3-6) |
静态加速度误差系数Ka:
 |
(3-7) |
将(3-5),(3-6)及(3-7)分别代入(3-2),(3-3)及(3-4)得
单位阶跃函数:
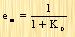 |
(3-8) |
单位斜坡函数:
 |
(3-9) |
单位加速度函数:
 |
(3-10) |
下面进一步考察误差系数与系统的结构和参数的关系。
系统开环传递函数一般写成
 |
(3-11) |
的形式,式中K是系统的开环比例系数。分母中的因子sυ表明开环传递函数中含有υ个积分单元。将系统按照υ=0,1,2分别将其分为0型,1型,2型。在表3-1中列出了按照式(3-2),(3-3)及(3-4)求得的系统稳态误差系数。
| |
0型系统 |
1型系统 |
2型系统 |
| (阶跃输入)r(t)=1(t) |
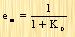 |
0 |
0 |
| (斜坡输入)r(t)=t/td>
| ∞ |
 |
0 |
| (加速度输入)r(t)=t2/2 |
∞ |
∞ |
 |
| 表3-1 0型、1型及2型系统以增益K表示的稳态误差 |
误差系数Kp、Kv和Ka描述了系统减少或消除稳态误差的能力,系数值愈大,则给定稳态误差终值愈小。一般来说,在保持瞬态响应在一个允许的范围内时,希望增加误差系数,如果在静态速度误差系数和加速度误差系数之间有任何矛盾时,主要考虑前者。
务请注意,使用拉普拉斯变换终值定理计算稳态误差终值的条件是:sEr(s)在s平面右半部及虚轴上除了坐标原点是孤立奇点外必需解析,亦即sEr(s)的全部极点除坐标原点外应全部分布在s平面的左半部。例如给定输入为正弦函数时
其象函数
在s平面的全部虚轴上不解析,就不能使用终值定理去求取系统的稳态误差终值。
3.2.4 动态误差
静态误差系数的一个明显特点,是对于一个给定系统只有一个系数呈现有限值,其它的系数不是零就是无穷大。因而,通过静态误差系数求得的静态误差或是零,或是有限的非零值,或是无穷大。所以,误差随时间的变化规律不能运用这种系数求出。但有些时候人们关心的往往是误差随时间变化的情况,这种误差表现了误差随时间变化的规律,称之为动态误差。本节介绍的动态误差将提供一些关于误差怎样随时间变化的信息,即,系统在给定的输入作用下稳态误差是否会与t,t2等成比例地增加。
动态误差不同但稳态误差系数相同的系统 首先论证两个具有不同动态误差的系统却能够有相同的静态误差系数。设以下的两个系统:
其静态误差系数由下列各式给出:
Kp1=∞, Kp2=∞
Kv1=10, Kv2=10
Ka1=0, Ka2=0
于是,对于同样的阶跃输入,两个系统有相同的稳态误差。当然,对于斜坡和抛物线输入的稳态误差,该结论也同样适用。这个分析表明,不能根据静态误差系数去估算系统的动态误差。
动态误差系数 现在引进动态误差系数来描述动态误差。通过用E(s)/R(s)的分母多项式除它的分子多项式的方法,把E(s)/R(s)展开成下列s的升幂级数:
幂级数的系数K1、K2、K3、…被定义为动态误差系数。对N型系统的动态误差系数由下式给出:
其中
K1=动态位置误差系数;
K2=动态速度误差系数;
K3=动态加速度误差系数。
需要说明的是,在一个给定系统中,动态误差系数是与静态误差系数有关的。例如:设下列具有单位反馈的0型系统:
其静态位置误差系数、静态速度误差系数和静态加速度误差系数分别是
其中
Kp=K
Kv=0
Ka=0
由于E(s)/R(s)可展开成
所以,依据静态误差系数给出的动态误差系数如下:
k1=1+K=1+Kp
动态速度误差系数由下式给出:
当E(s)写成下面的形式时:
E(s)= R(s)+ sR(s)+ s2R(s)+…
动态误差系数的优点就更为清楚。这个级数的收敛域是s=0的邻域,这相当于在时域内的t=∞。假定所有的初始条件为零,并且忽略掉在t=0的邻域,这相当于在时域内的t=∞。假定所有的初始条件为零,并且忽略掉在t=0时的脉冲,则对应的时间解(即稳态误差)由下式求出:
这样,由输入函数和它的导数所引起的稳态误差能根据动态误差系数求出,这便是动态误差系数的一个优点。
如果E(s)/R(s)围绕原点展开成一个幂级数,级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。
例3-9
设前向传递函数为G(s)=  的单位反馈控制系统,求出它的动态误差系数。还要求出当输入量为r(t)=a0+a1t+a2t2时的稳态误差。 的单位反馈控制系统,求出它的动态误差系数。还要求出当输入量为r(t)=a0+a1t+a2t2时的稳态误差。
对于该系统  = =  =0.1s+0.09s2-0.019s3+… =0.1s+0.09s2-0.019s3+…
即  =0.1 =0.1 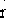 (t)+0.09 (t)+0.09 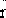 (t)-0.019 (t)-0.019  (t)+… (t)+…
则动态误差系数是 k1=∞
k2=1/0.1=10
k3=1/0.09=11.1
由于r(t)由下式给出:r(t)=a0+a1t+a2t2
得 (t)=a1+a2t, (t)=a1+a2t, (t)=2a2, (t)=2a2, (t)=0 (t)=0
于是,稳态误差为
 = =  [0.1(a1+a2t)+0.09(2a2)]= [0.1(a1+a2t)+0.09(2a2)]=  (0.1a1+0.18a2+0.2a2t) (0.1a1+0.18a2+0.2a2t)
只要不是a2=0,稳态误差就变为无穷大。
由以上分析可知,如果E(s)/R(s)围绕原点展开成一个幂级数,级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。 | 



















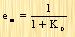












 电气控制与PLC_第2版
电气控制与PLC_第2版









 京公网安备 11010802033920号
京公网安备 11010802033920号