CAN调度理论与实践分析

CAN调度理论与实践分析

CAN总线中消息能否按时送达是事关系统安全等问题的重要指标，它要通过调度分析加以验证。本文介绍CAN调度理论的新研究成果，以及对工程应用的指导意义及其实施难点。具体分为4个部分：Tindell的分析方法和Davis的改进；笔者对Davis算法的简化；最坏响应时间分析在应用上的一些结果；调度分析在应用上的难处。

关键词  CAN  调度理论  响应时间  Davis算法  Tindell算法

　　分布式嵌入式系统是当前嵌入式系统的重要发展方向，因为它能提供更强的性能，节约系统的总体成本。但是由于各单个节点必须有通信网络相连才能协调地工作，网络就成了关键部分，没有网络提供及时正确的数据和命令，就谈不上所设计的系统服务了。在汽车的分布式嵌入式系统中，目前主流的通信网络是CAN总线。CAN是事件触发的通信协议，它根据消息的优先等级和节点的状态自动地调度消息的传送。低优先级的消息会因同时发生的高优先级消息太多而不能及时发送，高优先级消息也有可能由于节点状态等的影响而丢失。关于CAN的局限问题可见参考文献[1]。本文主要从调度理论方面讨论CAN系统的问题，这些问题与工程应用有非常大的关系，实践意义很强。

1  Tindell的分析方法和Davis的改进

　　1994年，Tindell [23]首先将分析单处理器任务调度方法改造成适用于CAN总线的调度方法，求取消息的最坏响应时间。对于与安全相关的应用，只有对最坏响应时间有确切的掌握，才是合理的。CAN通信在网络上的实现经过2个阶段：通信任务将消息发到发送的通信控制器(CC)，发送的通信控制器将消息发到接收的通信控制器。广义地讲，响应时间是从需产生通信的事件发生到消息到达目标节点的时间，包括发送节点host内的处理时间，host到CC的时间，总线上消息仲裁传送时间，接收CC到host的处理时间。仲裁获胜的消息开始传送后，便不能被中止，所以CAN调度是固定优先级非抢先式任务调度。消息m用到的参数定义如下:

　　Tm ——启动通信的事件间隔，即周期；
　　Jm——由事件发生到消息开始送CC的时间之最大变化，即抖动；
　　Cm—— 在总线上传送消息m所需时间（要考虑位填充形成的最大值）；
　　Dm——由应用决定的传送消息m允许的时限；
　　Rm——实际的最坏传送时间；
　　Wm——传送消息m时最坏等待时间。

　　它们之间的关系如图1所示。

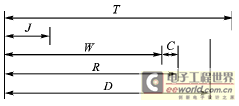
图1  用于调度分析的时间参数

　　Wm由2部分构成：由低于优先级m的消息（其集合写为lp(m)）正在总线上传送而造成的阻塞Bm，和由高于优先级m的消息（其集合写为hp(m)）在总线上抢先传送而造成的干扰Im。它们取最大值时就使Wm成为最坏等待时间。

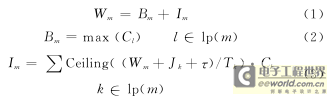
　　为了印刷的方便和易于理解，这里用了不同的写法，其中顶函数Ceiling返回的是最接近（大于等于）变量的上限整数, τ是1位时间。Ceiling( (Wm+Jk+τ)/Tk)表示在Wm时段内高优先级消息k会出现的最多次数。于是有：

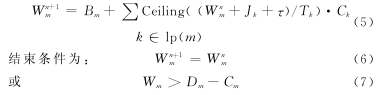
　　Wm取离散值且出现在非线性方程(4)的两边，所幸的是其求解并不难。在式(5)中，用W0m=Bm作为初值循环求解即可。

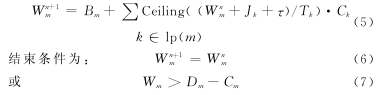
　　式(7)代表最坏等待时间已超时限，消息m不可调度。

　　按优先级降低的次序逐条校验消息是否可调度，就可验证整个通信系统是否可调度。

　　在2006年实时网络会议上，Bril、Davis等人发表了有关Tindell算法有漏洞的文章，后来他们又提出了完整的改进算法[4]。作为反例，表1中消息C用Tindell算法是可调度的，最坏响应时间为3 ms；但第2次消息C的传送已超时限，如图2所示。Tindell算法仅考虑了消息C的第1次传送。

表1  Tindell算法的反例

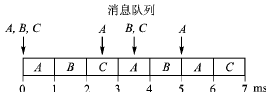
图2  消息C的最坏响应时间为3.5 ms

　　另外，如将消息B和C的周期缩短为3.25 ms，按照Tindell算法，系统由于未求得最大的最坏响应时间，故仍是可调度的，但实际上总线的利用率已超过100%。Davis的方法核心是引入忙周期的概念，再对忙周期内各次传送的响应时间求最坏值，详见附录1。（见本刊网站www.mesnet.com.cn——编者注。）

　　Tindell的开创性工作对后续的研究与应用有巨大的影响，Volcano通信技术公司(现在的Mentor Graphics)以此理论为基础开发了商用的CAN调度分析软件。由于漏洞的发现，用户应检验软件是否有了新的补丁以及用它完成的应用是否受影响。

2  笔者对Davis算法的简化

　　Davis算法要先算出忙周期，再在忙周期中消息m多次传送中寻找最坏等待最大的那次。基于以下考虑，计算可以简化：

　　在忙周期中，消息m传送时有高优先级消息进入队列，使m的后续消息发送前可能插入更多的高优先级消息，代表仍有一个对总线需求的高峰，从而有可能使后面的消息m有更大的最坏响应时间。

　　最坏的情形是消息m刚发送，所有高优先级消息就进入队列，即领先于发完消息m后的第一个发送空隙的相位达到最大。

　　因此求消息m的最坏响应时间就有两种可能： 用Bm产生阻塞，像Tindell那样求消息m的最坏响应时间；由Cm产生阻塞，求下一个消息m的最坏响应时间，下一个消息m的排队时间为Tm-Jm。

　　简化方法的优点是减少了计算的次数，从而减少工作量。

　　这种算法与Davis算法中的保守算法有两点不同：一是用Cm来产生阻塞是真实可能发生的，例如从休眠到上电时消息m比高优先级消息早了一点；二是本算法得到的是确切的而非保守的结果。