摘要:利用SVM(Support Vector Machine)解决二类分类问题的优势,设计了一个粗细两级指纹分类体器,提出了并实现了一种新型的指纹分类算法。测量结果表明,该分类器具有很好的泛化能力,对于新样本分类的正确率达98.5%,具有一定的实用价值。
关键词:指纹分类 分类器 特征提取 支持向量机
指纹作为个人身份的标志具有唯一性和终生不变性。随着计算机技术的发展,指纹识别技术成为目前使用最广泛的物生识别技术。一个典型的自动指纹识别系统通常包括五部分:采样、预处理、特征提取、分类和细节匹配。指纹分类环节对于分解整个复杂的识别任务、缩小细节匹配的范围和提高提高识别的效率都具有非常重要的意义。分类算法取决于特征提取环节,大致发为以下五种:
%26;#183;语法分析法(Syntactic Approach);
%26;#183;几何法(Geometry Approach)
%26;#183;随机法(Stochastic Approach);
%26;#183;神经网络法(Neral Network Approach);
%26;#183;基于奇异点的分类法(Singularity-based Approach)。
 神经网络方法在指纹识别技术中应用较为广泛,但是由于理论本身存储在缺陷,神经网络法容易陷入局部最优和过学习。本文算法的理论基于——SVM方法拥有严密的数字解释,因此,与神经网络方法相比推广能力大大提高。
目前,SVM理论在指纹分类中的应用并不多:王崇文等人提出了一种基于隐马尔可夫模型和支持向量机的两级分类方法;Shesha Shah等人利用五个SVM分类器将指纹分成了五类,其中分类的原则是反馈型线检测器的特征提取。该算法中普通弓形和帐弓形的指纹对于新样本的范化能力不理想,正确率只有79.10%。本文设计的基于支持向量机理论粗细二级分类,使用五个SVM分类器,充分利用它们进行二类分类的优势,将指纹分为六类。本算法对于新样本的范化能力有明显提高,其中弓形分类的正确率可以达到96.7%。本文从四个方面阐述基于支持向量机理论的二级指纹分类算法。SVM这一新的理论不仅为将来指纹分类工作的研究提代了坚实的理论基础,而且给算法的简化和不断完善开拓了崭新的思路。
1 支持向量机理论
支持向量机是贝尔实验室研究人员V.Vapnik等人在对统计学习理论多年的研究基础上发展起来的一种全新的机器学习算法。机器学习的实际风险由两部分构成:经验风险和置信范围,其中后者与Vapnik提出的VC维的概念有关。传统的使用经验风险最小化ERM(Empirical Risk Minimization)的分类训练方法,虽然能取得小的经验风险,但置信范围很大,导致过学习,推广能力下降。SVM方法建立在编译学习的VC维(Vapnik Chervonenkis Dimension)理论和结构风险最小化原理SRM(Structural Risk Minimization)基础上,兼顾了两部分风险构成,把函数构造为一个函数子集序列,在子集间折衷考虑经验风险和置信范围,可以使实际风险最小。
神经网络方法在指纹识别技术中应用较为广泛,但是由于理论本身存储在缺陷,神经网络法容易陷入局部最优和过学习。本文算法的理论基于——SVM方法拥有严密的数字解释,因此,与神经网络方法相比推广能力大大提高。
目前,SVM理论在指纹分类中的应用并不多:王崇文等人提出了一种基于隐马尔可夫模型和支持向量机的两级分类方法;Shesha Shah等人利用五个SVM分类器将指纹分成了五类,其中分类的原则是反馈型线检测器的特征提取。该算法中普通弓形和帐弓形的指纹对于新样本的范化能力不理想,正确率只有79.10%。本文设计的基于支持向量机理论粗细二级分类,使用五个SVM分类器,充分利用它们进行二类分类的优势,将指纹分为六类。本算法对于新样本的范化能力有明显提高,其中弓形分类的正确率可以达到96.7%。本文从四个方面阐述基于支持向量机理论的二级指纹分类算法。SVM这一新的理论不仅为将来指纹分类工作的研究提代了坚实的理论基础,而且给算法的简化和不断完善开拓了崭新的思路。
1 支持向量机理论
支持向量机是贝尔实验室研究人员V.Vapnik等人在对统计学习理论多年的研究基础上发展起来的一种全新的机器学习算法。机器学习的实际风险由两部分构成:经验风险和置信范围,其中后者与Vapnik提出的VC维的概念有关。传统的使用经验风险最小化ERM(Empirical Risk Minimization)的分类训练方法,虽然能取得小的经验风险,但置信范围很大,导致过学习,推广能力下降。SVM方法建立在编译学习的VC维(Vapnik Chervonenkis Dimension)理论和结构风险最小化原理SRM(Structural Risk Minimization)基础上,兼顾了两部分风险构成,把函数构造为一个函数子集序列,在子集间折衷考虑经验风险和置信范围,可以使实际风险最小。
 本文设计的粗细二级分类使用五个SVM分类器,其中两个将指纹粗分为三类,另外三个将指纹细分为六类,SVM分类器解决的都是二类分类问题。
2 算法实现步骤
2.1 特征提取
指纹图像通过预处理后,已经是二值化和细化后图像,见图1。
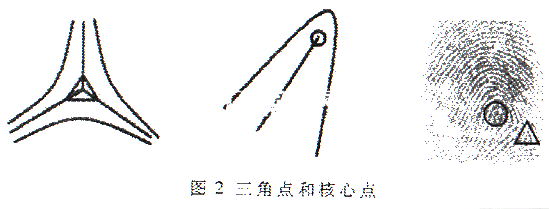
要分析指纹图像,首先需进行特征提取。本文采用基于奇异点的特征提取。指纹的特片分为两 种:全局特征和局部细节特征。前者用于指纹分类,后者用于细节匹配。全局特片点即奇异点包括:三角点(delta)和核心点(core),见图2。三角点位于从核心点两个方向差别较大的纹路的汇聚处;核心点位于指纹纹路的渐进中心,它是指纹中心脊线上曲率最大的点。
本文设计的粗细二级分类使用五个SVM分类器,其中两个将指纹粗分为三类,另外三个将指纹细分为六类,SVM分类器解决的都是二类分类问题。
2 算法实现步骤
2.1 特征提取
指纹图像通过预处理后,已经是二值化和细化后图像,见图1。
要分析指纹图像,首先需进行特征提取。本文采用基于奇异点的特征提取。指纹的特片分为两 种:全局特征和局部细节特征。前者用于指纹分类,后者用于细节匹配。全局特片点即奇异点包括:三角点(delta)和核心点(core),见图2。三角点位于从核心点两个方向差别较大的纹路的汇聚处;核心点位于指纹纹路的渐进中心,它是指纹中心脊线上曲率最大的点。
 2.2 根据特征提取设计分类器
指纹通常可以分成五类:斗型、右旋、左旋、拱形和帐篷形。为了更好地发挥SVM算法解决二类分类问题的优势,本文设计了一个两级分类器,结构框架见图3。分类器包括粗分类和细分类两级。第一级将指纹粗分为:斗形(Whor1)、旋形(Loop)和弓形(Arch)三类;第二级,弓形细分为普通弓形(Normal Arch)和帐弓形(Tented Arch),旋形细分为左旋(Left Loop)和右旋(Right Loop),斗形细分为单斗(Single Whorl)和双斗(Twins Whorl)。
2.3 分类判别准则
第一级粗分类遵循如下原则:
%26;#183;分离斗形,分类准则:核心点的个数(只有斗形的核心点是两个);
%26;#183;区分旋形和弓形,分类准则:两者虽然拥有同样的奇异点(一个核心点和个三角点),奇导点的连线相对于图像参考轴的夹角不同。
第二级细分类均为二类分类问题。细分依据分别为:
%26;#183;斗形:两核心点的连线与图像参考轴的相对位置;
%26;#183;旋形:核心点和三角点连线与图像参考轴的夹角;
%26;#183;弓形:核心点的数目。
2.4 SVM分类器
根据两级分类的判别标准决定SVM的n维输入向量X(x1,x2,…xn)的维数,训练样本(x1,y1),…,(xn,yn),x∈Rn,y∈{+1,-1}服从某个未知的概率分布,通过对样本归一化,求解最优的分类超平面:
yi(xi%26;#183;W+b) -1≥0 (1)
并且使分类间隔1/||W||最大,从而将两类样本无误地分开。这是一个线性约束的二次规划问题,利用Lagrange函数:
2.2 根据特征提取设计分类器
指纹通常可以分成五类:斗型、右旋、左旋、拱形和帐篷形。为了更好地发挥SVM算法解决二类分类问题的优势,本文设计了一个两级分类器,结构框架见图3。分类器包括粗分类和细分类两级。第一级将指纹粗分为:斗形(Whor1)、旋形(Loop)和弓形(Arch)三类;第二级,弓形细分为普通弓形(Normal Arch)和帐弓形(Tented Arch),旋形细分为左旋(Left Loop)和右旋(Right Loop),斗形细分为单斗(Single Whorl)和双斗(Twins Whorl)。
2.3 分类判别准则
第一级粗分类遵循如下原则:
%26;#183;分离斗形,分类准则:核心点的个数(只有斗形的核心点是两个);
%26;#183;区分旋形和弓形,分类准则:两者虽然拥有同样的奇异点(一个核心点和个三角点),奇导点的连线相对于图像参考轴的夹角不同。
第二级细分类均为二类分类问题。细分依据分别为:
%26;#183;斗形:两核心点的连线与图像参考轴的相对位置;
%26;#183;旋形:核心点和三角点连线与图像参考轴的夹角;
%26;#183;弓形:核心点的数目。
2.4 SVM分类器
根据两级分类的判别标准决定SVM的n维输入向量X(x1,x2,…xn)的维数,训练样本(x1,y1),…,(xn,yn),x∈Rn,y∈{+1,-1}服从某个未知的概率分布,通过对样本归一化,求解最优的分类超平面:
yi(xi%26;#183;W+b) -1≥0 (1)
并且使分类间隔1/||W||最大,从而将两类样本无误地分开。这是一个线性约束的二次规划问题,利用Lagrange函数:

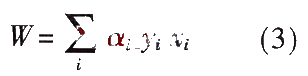 解出支持向量α,再将带入(1)式,确定最优超平面,将两类正确地分开。以旋形的细分类为例,首先根据分类的判断准则确定输入向量的维数,这里输入向量X是三维,包括三角点相对横坐标x1、相对纵坐标x2、三角点和核心点连线与图像参考轴的夹角x3,即X(x1,x2,x3)。然后根据上述公式求解出支持向量α,最终确定将左旋和右旋正确分开的超平面。
3 实验结果
实验使用了FVC2004的指纹数据库和晶体2100型指纹采集仪,抽取不同数目的指纹作为训练样本,使用Microsoft Visual Studio.Net2003编程实现了使用SVM方法的二级指纹分类。选取的样本容量以及分类正确率,见表1。对于新样本SVM方法表现出了很好的泛化能力,分类判别的正确率大大提高,而且由于实现的是二级粗细分类,需要进行判断样本的数目分流,加快了分类的速度。通过验证不同容量的训练样本可以得出结论,SVM方法在解决二类分类问题上的确有优于其他算法之处。
表1 两级分类正确率统计
项目
种类
训练样本的
容量
精确度(%)
项目
种类
训练样本的
容量
新样本的容量
精确度(%)
A
100
100
NA
50
25
96.7
TA
50
25
96.5
L
300
99.8
LL
150
75
96.3
RL
150
75
99.6
W
200
99.9
SW
100
50
98.2
TW
100
50
97.9
SVM方法不但能提高分类的速率,而且不限制模型的选择。SVM有三种不同的内核函数:(1)多项式核函数(polynomial):K(x,xi)=[x%26;#183;xi]+q;(2)径向基函数(Radial Basis Function);
解出支持向量α,再将带入(1)式,确定最优超平面,将两类正确地分开。以旋形的细分类为例,首先根据分类的判断准则确定输入向量的维数,这里输入向量X是三维,包括三角点相对横坐标x1、相对纵坐标x2、三角点和核心点连线与图像参考轴的夹角x3,即X(x1,x2,x3)。然后根据上述公式求解出支持向量α,最终确定将左旋和右旋正确分开的超平面。
3 实验结果
实验使用了FVC2004的指纹数据库和晶体2100型指纹采集仪,抽取不同数目的指纹作为训练样本,使用Microsoft Visual Studio.Net2003编程实现了使用SVM方法的二级指纹分类。选取的样本容量以及分类正确率,见表1。对于新样本SVM方法表现出了很好的泛化能力,分类判别的正确率大大提高,而且由于实现的是二级粗细分类,需要进行判断样本的数目分流,加快了分类的速度。通过验证不同容量的训练样本可以得出结论,SVM方法在解决二类分类问题上的确有优于其他算法之处。
表1 两级分类正确率统计
项目
种类
训练样本的
容量
精确度(%)
项目
种类
训练样本的
容量
新样本的容量
精确度(%)
A
100
100
NA
50
25
96.7
TA
50
25
96.5
L
300
99.8
LL
150
75
96.3
RL
150
75
99.6
W
200
99.9
SW
100
50
98.2
TW
100
50
97.9
SVM方法不但能提高分类的速率,而且不限制模型的选择。SVM有三种不同的内核函数:(1)多项式核函数(polynomial):K(x,xi)=[x%26;#183;xi]+q;(2)径向基函数(Radial Basis Function);
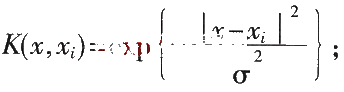 (3)Sigmoid函数:K(x,xi)=tanh(v(x%26;#183;xi)+c)。实验使用三种函数的模型对弓形进行细分类,训练样本容量选取100,数据见表2,其中统计了两类的支持向量的数目分别用Positive_SVM和Negative_SVM表示。
表2 验证三种核函数
内核函数
Total_SV
Positive_SV
Negative_SV
精确度(%)
polynomial
98
53
45
96.3
RBF
20
9
11
96.5
sigmoid
90
45
45
96.7
实验结果表明,核函数的选取对分类的效果影响甚小,因此算法在模型的选择具有很大的灵活性。
实验表明,将支持向量机理论应用于指纹分类是可行的,而且对于提高指纹分类算法的效率有不可或缺的作用。SVM方法基于严密的数学理论,遵循SRM原则寻找最优超平面。本文设计的粗细二级分类器,将指纹先后分成了三类和六类,充分发挥了SVM理论解决二类分类问题的优势,通过编程实现,训练样本具有较好的泛化能力。与神经网络方法相比,本文提出的算法无论是在理论基础方面还是在模型选择的灵活性方面都表现出了极大的优越性。
(3)Sigmoid函数:K(x,xi)=tanh(v(x%26;#183;xi)+c)。实验使用三种函数的模型对弓形进行细分类,训练样本容量选取100,数据见表2,其中统计了两类的支持向量的数目分别用Positive_SVM和Negative_SVM表示。
表2 验证三种核函数
内核函数
Total_SV
Positive_SV
Negative_SV
精确度(%)
polynomial
98
53
45
96.3
RBF
20
9
11
96.5
sigmoid
90
45
45
96.7
实验结果表明,核函数的选取对分类的效果影响甚小,因此算法在模型的选择具有很大的灵活性。
实验表明,将支持向量机理论应用于指纹分类是可行的,而且对于提高指纹分类算法的效率有不可或缺的作用。SVM方法基于严密的数学理论,遵循SRM原则寻找最优超平面。本文设计的粗细二级分类器,将指纹先后分成了三类和六类,充分发挥了SVM理论解决二类分类问题的优势,通过编程实现,训练样本具有较好的泛化能力。与神经网络方法相比,本文提出的算法无论是在理论基础方面还是在模型选择的灵活性方面都表现出了极大的优越性。
编辑: 引用地址:基于SVM的两纺指纹分类研究
 神经网络方法在指纹识别技术中应用较为广泛,但是由于理论本身存储在缺陷,神经网络法容易陷入局部最优和过学习。本文算法的理论基于——SVM方法拥有严密的数字解释,因此,与神经网络方法相比推广能力大大提高。
目前,SVM理论在指纹分类中的应用并不多:王崇文等人提出了一种基于隐马尔可夫模型和支持向量机的两级分类方法;Shesha Shah等人利用五个SVM分类器将指纹分成了五类,其中分类的原则是反馈型线检测器的特征提取。该算法中普通弓形和帐弓形的指纹对于新样本的范化能力不理想,正确率只有79.10%。本文设计的基于支持向量机理论粗细二级分类,使用五个SVM分类器,充分利用它们进行二类分类的优势,将指纹分为六类。本算法对于新样本的范化能力有明显提高,其中弓形分类的正确率可以达到96.7%。本文从四个方面阐述基于支持向量机理论的二级指纹分类算法。SVM这一新的理论不仅为将来指纹分类工作的研究提代了坚实的理论基础,而且给算法的简化和不断完善开拓了崭新的思路。
1 支持向量机理论
支持向量机是贝尔实验室研究人员V.Vapnik等人在对统计学习理论多年的研究基础上发展起来的一种全新的机器学习算法。机器学习的实际风险由两部分构成:经验风险和置信范围,其中后者与Vapnik提出的VC维的概念有关。传统的使用经验风险最小化ERM(Empirical Risk Minimization)的分类训练方法,虽然能取得小的经验风险,但置信范围很大,导致过学习,推广能力下降。SVM方法建立在编译学习的VC维(Vapnik Chervonenkis Dimension)理论和结构风险最小化原理SRM(Structural Risk Minimization)基础上,兼顾了两部分风险构成,把函数构造为一个函数子集序列,在子集间折衷考虑经验风险和置信范围,可以使实际风险最小。
神经网络方法在指纹识别技术中应用较为广泛,但是由于理论本身存储在缺陷,神经网络法容易陷入局部最优和过学习。本文算法的理论基于——SVM方法拥有严密的数字解释,因此,与神经网络方法相比推广能力大大提高。
目前,SVM理论在指纹分类中的应用并不多:王崇文等人提出了一种基于隐马尔可夫模型和支持向量机的两级分类方法;Shesha Shah等人利用五个SVM分类器将指纹分成了五类,其中分类的原则是反馈型线检测器的特征提取。该算法中普通弓形和帐弓形的指纹对于新样本的范化能力不理想,正确率只有79.10%。本文设计的基于支持向量机理论粗细二级分类,使用五个SVM分类器,充分利用它们进行二类分类的优势,将指纹分为六类。本算法对于新样本的范化能力有明显提高,其中弓形分类的正确率可以达到96.7%。本文从四个方面阐述基于支持向量机理论的二级指纹分类算法。SVM这一新的理论不仅为将来指纹分类工作的研究提代了坚实的理论基础,而且给算法的简化和不断完善开拓了崭新的思路。
1 支持向量机理论
支持向量机是贝尔实验室研究人员V.Vapnik等人在对统计学习理论多年的研究基础上发展起来的一种全新的机器学习算法。机器学习的实际风险由两部分构成:经验风险和置信范围,其中后者与Vapnik提出的VC维的概念有关。传统的使用经验风险最小化ERM(Empirical Risk Minimization)的分类训练方法,虽然能取得小的经验风险,但置信范围很大,导致过学习,推广能力下降。SVM方法建立在编译学习的VC维(Vapnik Chervonenkis Dimension)理论和结构风险最小化原理SRM(Structural Risk Minimization)基础上,兼顾了两部分风险构成,把函数构造为一个函数子集序列,在子集间折衷考虑经验风险和置信范围,可以使实际风险最小。
 本文设计的粗细二级分类使用五个SVM分类器,其中两个将指纹粗分为三类,另外三个将指纹细分为六类,SVM分类器解决的都是二类分类问题。
2 算法实现步骤
2.1 特征提取
指纹图像通过预处理后,已经是二值化和细化后图像,见图1。
要分析指纹图像,首先需进行特征提取。本文采用基于奇异点的特征提取。指纹的特片分为两 种:全局特征和局部细节特征。前者用于指纹分类,后者用于细节匹配。全局特片点即奇异点包括:三角点(delta)和核心点(core),见图2。三角点位于从核心点两个方向差别较大的纹路的汇聚处;核心点位于指纹纹路的渐进中心,它是指纹中心脊线上曲率最大的点。
本文设计的粗细二级分类使用五个SVM分类器,其中两个将指纹粗分为三类,另外三个将指纹细分为六类,SVM分类器解决的都是二类分类问题。
2 算法实现步骤
2.1 特征提取
指纹图像通过预处理后,已经是二值化和细化后图像,见图1。
要分析指纹图像,首先需进行特征提取。本文采用基于奇异点的特征提取。指纹的特片分为两 种:全局特征和局部细节特征。前者用于指纹分类,后者用于细节匹配。全局特片点即奇异点包括:三角点(delta)和核心点(core),见图2。三角点位于从核心点两个方向差别较大的纹路的汇聚处;核心点位于指纹纹路的渐进中心,它是指纹中心脊线上曲率最大的点。
 2.2 根据特征提取设计分类器
指纹通常可以分成五类:斗型、右旋、左旋、拱形和帐篷形。为了更好地发挥SVM算法解决二类分类问题的优势,本文设计了一个两级分类器,结构框架见图3。分类器包括粗分类和细分类两级。第一级将指纹粗分为:斗形(Whor1)、旋形(Loop)和弓形(Arch)三类;第二级,弓形细分为普通弓形(Normal Arch)和帐弓形(Tented Arch),旋形细分为左旋(Left Loop)和右旋(Right Loop),斗形细分为单斗(Single Whorl)和双斗(Twins Whorl)。
2.3 分类判别准则
第一级粗分类遵循如下原则:
%26;#183;分离斗形,分类准则:核心点的个数(只有斗形的核心点是两个);
%26;#183;区分旋形和弓形,分类准则:两者虽然拥有同样的奇异点(一个核心点和个三角点),奇导点的连线相对于图像参考轴的夹角不同。
第二级细分类均为二类分类问题。细分依据分别为:
%26;#183;斗形:两核心点的连线与图像参考轴的相对位置;
%26;#183;旋形:核心点和三角点连线与图像参考轴的夹角;
%26;#183;弓形:核心点的数目。
2.4 SVM分类器
根据两级分类的判别标准决定SVM的n维输入向量X(x1,x2,…xn)的维数,训练样本(x1,y1),…,(xn,yn),x∈Rn,y∈{+1,-1}服从某个未知的概率分布,通过对样本归一化,求解最优的分类超平面:
yi(xi%26;#183;W+b) -1≥0 (1)
并且使分类间隔1/||W||最大,从而将两类样本无误地分开。这是一个线性约束的二次规划问题,利用Lagrange函数:
2.2 根据特征提取设计分类器
指纹通常可以分成五类:斗型、右旋、左旋、拱形和帐篷形。为了更好地发挥SVM算法解决二类分类问题的优势,本文设计了一个两级分类器,结构框架见图3。分类器包括粗分类和细分类两级。第一级将指纹粗分为:斗形(Whor1)、旋形(Loop)和弓形(Arch)三类;第二级,弓形细分为普通弓形(Normal Arch)和帐弓形(Tented Arch),旋形细分为左旋(Left Loop)和右旋(Right Loop),斗形细分为单斗(Single Whorl)和双斗(Twins Whorl)。
2.3 分类判别准则
第一级粗分类遵循如下原则:
%26;#183;分离斗形,分类准则:核心点的个数(只有斗形的核心点是两个);
%26;#183;区分旋形和弓形,分类准则:两者虽然拥有同样的奇异点(一个核心点和个三角点),奇导点的连线相对于图像参考轴的夹角不同。
第二级细分类均为二类分类问题。细分依据分别为:
%26;#183;斗形:两核心点的连线与图像参考轴的相对位置;
%26;#183;旋形:核心点和三角点连线与图像参考轴的夹角;
%26;#183;弓形:核心点的数目。
2.4 SVM分类器
根据两级分类的判别标准决定SVM的n维输入向量X(x1,x2,…xn)的维数,训练样本(x1,y1),…,(xn,yn),x∈Rn,y∈{+1,-1}服从某个未知的概率分布,通过对样本归一化,求解最优的分类超平面:
yi(xi%26;#183;W+b) -1≥0 (1)
并且使分类间隔1/||W||最大,从而将两类样本无误地分开。这是一个线性约束的二次规划问题,利用Lagrange函数:

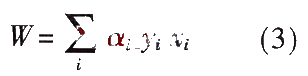 解出支持向量α,再将带入(1)式,确定最优超平面,将两类正确地分开。以旋形的细分类为例,首先根据分类的判断准则确定输入向量的维数,这里输入向量X是三维,包括三角点相对横坐标x1、相对纵坐标x2、三角点和核心点连线与图像参考轴的夹角x3,即X(x1,x2,x3)。然后根据上述公式求解出支持向量α,最终确定将左旋和右旋正确分开的超平面。
3 实验结果
实验使用了FVC2004的指纹数据库和晶体2100型指纹采集仪,抽取不同数目的指纹作为训练样本,使用Microsoft Visual Studio.Net2003编程实现了使用SVM方法的二级指纹分类。选取的样本容量以及分类正确率,见表1。对于新样本SVM方法表现出了很好的泛化能力,分类判别的正确率大大提高,而且由于实现的是二级粗细分类,需要进行判断样本的数目分流,加快了分类的速度。通过验证不同容量的训练样本可以得出结论,SVM方法在解决二类分类问题上的确有优于其他算法之处。
表1 两级分类正确率统计
项目
种类
训练样本的
容量
精确度(%)
项目
种类
训练样本的
容量
新样本的容量
精确度(%)
A
100
100
NA
50
25
96.7
TA
50
25
96.5
L
300
99.8
LL
150
75
96.3
RL
150
75
99.6
W
200
99.9
SW
100
50
98.2
TW
100
50
97.9
SVM方法不但能提高分类的速率,而且不限制模型的选择。SVM有三种不同的内核函数:(1)多项式核函数(polynomial):K(x,xi)=[x%26;#183;xi]+q;(2)径向基函数(Radial Basis Function);
解出支持向量α,再将带入(1)式,确定最优超平面,将两类正确地分开。以旋形的细分类为例,首先根据分类的判断准则确定输入向量的维数,这里输入向量X是三维,包括三角点相对横坐标x1、相对纵坐标x2、三角点和核心点连线与图像参考轴的夹角x3,即X(x1,x2,x3)。然后根据上述公式求解出支持向量α,最终确定将左旋和右旋正确分开的超平面。
3 实验结果
实验使用了FVC2004的指纹数据库和晶体2100型指纹采集仪,抽取不同数目的指纹作为训练样本,使用Microsoft Visual Studio.Net2003编程实现了使用SVM方法的二级指纹分类。选取的样本容量以及分类正确率,见表1。对于新样本SVM方法表现出了很好的泛化能力,分类判别的正确率大大提高,而且由于实现的是二级粗细分类,需要进行判断样本的数目分流,加快了分类的速度。通过验证不同容量的训练样本可以得出结论,SVM方法在解决二类分类问题上的确有优于其他算法之处。
表1 两级分类正确率统计
项目
种类
训练样本的
容量
精确度(%)
项目
种类
训练样本的
容量
新样本的容量
精确度(%)
A
100
100
NA
50
25
96.7
TA
50
25
96.5
L
300
99.8
LL
150
75
96.3
RL
150
75
99.6
W
200
99.9
SW
100
50
98.2
TW
100
50
97.9
SVM方法不但能提高分类的速率,而且不限制模型的选择。SVM有三种不同的内核函数:(1)多项式核函数(polynomial):K(x,xi)=[x%26;#183;xi]+q;(2)径向基函数(Radial Basis Function);
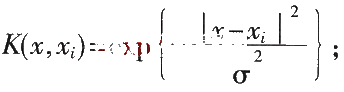 (3)Sigmoid函数:K(x,xi)=tanh(v(x%26;#183;xi)+c)。实验使用三种函数的模型对弓形进行细分类,训练样本容量选取100,数据见表2,其中统计了两类的支持向量的数目分别用Positive_SVM和Negative_SVM表示。
表2 验证三种核函数
内核函数
Total_SV
Positive_SV
Negative_SV
精确度(%)
polynomial
98
53
45
96.3
RBF
20
9
11
96.5
sigmoid
90
45
45
96.7
实验结果表明,核函数的选取对分类的效果影响甚小,因此算法在模型的选择具有很大的灵活性。
实验表明,将支持向量机理论应用于指纹分类是可行的,而且对于提高指纹分类算法的效率有不可或缺的作用。SVM方法基于严密的数学理论,遵循SRM原则寻找最优超平面。本文设计的粗细二级分类器,将指纹先后分成了三类和六类,充分发挥了SVM理论解决二类分类问题的优势,通过编程实现,训练样本具有较好的泛化能力。与神经网络方法相比,本文提出的算法无论是在理论基础方面还是在模型选择的灵活性方面都表现出了极大的优越性。
(3)Sigmoid函数:K(x,xi)=tanh(v(x%26;#183;xi)+c)。实验使用三种函数的模型对弓形进行细分类,训练样本容量选取100,数据见表2,其中统计了两类的支持向量的数目分别用Positive_SVM和Negative_SVM表示。
表2 验证三种核函数
内核函数
Total_SV
Positive_SV
Negative_SV
精确度(%)
polynomial
98
53
45
96.3
RBF
20
9
11
96.5
sigmoid
90
45
45
96.7
实验结果表明,核函数的选取对分类的效果影响甚小,因此算法在模型的选择具有很大的灵活性。
实验表明,将支持向量机理论应用于指纹分类是可行的,而且对于提高指纹分类算法的效率有不可或缺的作用。SVM方法基于严密的数学理论,遵循SRM原则寻找最优超平面。本文设计的粗细二级分类器,将指纹先后分成了三类和六类,充分发挥了SVM理论解决二类分类问题的优势,通过编程实现,训练样本具有较好的泛化能力。与神经网络方法相比,本文提出的算法无论是在理论基础方面还是在模型选择的灵活性方面都表现出了极大的优越性。
上一篇:精密控制系统中步进电机的电细分技术研究
下一篇:白噪声序列检验的小波分析方法

 嵌入式网络那些事:LwIP协议深度剖析与实战演练
嵌入式网络那些事:LwIP协议深度剖析与实战演练 LT1794IFE#PBF
LT1794IFE#PBF










 京公网安备 11010802033920号
京公网安备 11010802033920号