基于Taylor级数近似补偿的改进数控振荡器实现

　　引言

　　数字控制振荡器 (NCO) 在软件无线电(SDR)通信系统中具有重要的作用，是软件无线电数字变频技术的必要组成部分，它的性能很大程度上决定着数字变频模块性能以及载波同步模块的同步效果。在软件无线电通信中，信号的处理往往都集中在离散数字域内进行，数据的传输速率和信号的质量都要非常高，这样就要求数字控制振荡器必须具有频率分辨率高、频率转换速度快、无杂散动态范围值(SFDR)高、频谱纯度高和生成的正、余弦信号保持良好的正交特性等特点。

　　数控振荡器主要由相位累加器、量化器、相位幅度转换电路等部分组成。相位累加器将相位按频率控制字的步长累加，累加结果与初始相位(即相位偏移)的和作为量化器的输入，量化器截取前M bits作为相位幅度转换电路的输入，最后，相位幅度转换电路根据相位值输出对应的正弦或余弦值。本文通过对传统CORDIC算法实现数控振荡器存在的问题进行分析，提出一种适用于软件无线电通信系统的数控振荡器实现新方法。该方法利用二阶泰勒(Taylor)级数近似和残余相角补偿的方法来解决CORDIC算法实现时的精度不够的缺陷，提高了数控振荡器的输出信号频谱的纯度;整个设计采用流水线结构从而可以保证系统的高速度，满足软件无线电系统的高速数据处理的要求;在相位累加器部分加入相角抖动模块来改善角度周期性截断误差所引起的杂散，进一步提高数控振荡器的无杂散动态值。

　　传统CORDIC算法实现

　　CORDIC(Coordinate Rotation Digital Computer)算法是由J.Voider等人在1959年提出的[1]，它是基于向量旋转的算法，通过迭代方法实现对任意角度的向量旋转，这些迭代只需使用简单的移位和加减法操作，所有三角函数都可以通过向量旋转函数进行计算。CORDIC算法的基本迭代算式为：

　　用CORDIC算法实现数控振荡器存在精度不高的问题，它的杂散源主要有以下几部分：由于算法采用的算术精度有限对最终结果造成的误差，这部分误差是由尾数舍弃带来的截断误差，这部分误差是引起杂散的一个原因;N次旋转所得的累加角度与目标角度之间的残余相角误差所引起杂散;由于CORDIC算法的迭代级数有限，旋转产生的角度误差为周期信号，周期性误差同样会引起杂散。

　　由于传统CORDIC算法实现数控振荡器存在着不足，故本文在传统CORDIC算法的基础上，提出采用Taylor级数补偿CORDIC算法的改进数控振荡器实现方法。

　　基于Taylor级数近似补偿的改进实现数控振荡器

　　针对CORDIC算法在实现数控振荡器时存在的迭代残余角度误差、尾数舍入误差以及周期性误差的问题，本文提出了基于对这三部分误差补偿的改进实现方法。

　　周期性误差补偿

　　由于CORDIC算法的迭代级数有限，旋转产生的角度误差为周期信号，这样周期性误差会引起杂散，为了减少杂散，提高SFDR，在改进的数控振荡器中加入相位抖动模块。

　　相位抖动(Dither)的作用是在累加器输出加入随机信号，破坏累加相位的周期性。在累加器输出加入随机抖动信号，破坏累加相位的周期性，可以使数控振荡器输出端的杂散信号能够得到抑制。加入抖动模块可以提高SFDR值，但是杂散的抑制是以牺牲整个系统的基底误差(error floor)为代价的。杂散信号得到抑制的同时，信号的整个SNR会降低。因此抖动信号的幅度选取应合适。相位抖动范围太大会损失SFDR，太小时不能达到抑制杂散频率的效果[3]。相位抖动在实现时采用线性反馈移位寄存器(LFSR)生成伪随机信号序列，相位抖动模块输出的随机信号序列是[0,]范围内的随机值，其中，k为截断相位位宽。

　　迭代残余角度误差补偿

　　假设输入CORDIC模块的相角为，经过N次迭代后累加相角为，残余角度为：

　　这样就可以用公式7来补偿迭代残余角度误差引起的杂散，在方法实现时迭代残余角度误差补偿作为第一级补偿。

　　基于Taylor级数近似补偿的改进数控振荡器实现

　　在实现的时候，本文把CORDIC迭代后残余相角补偿作为第一级补偿模块，泰勒级数作为第二级补偿，同时为了降低CORDIC算法旋转产生的角度周期性误差，在设计数控振荡器时，在相位累加器部分引入了随机信号产生模块用来改善角度周期性误差所引起的杂散。基于改进CORDIC算法的数控振荡器的结构如图1所示，主要有相位累加器部分、随机信号产生模块、残余相角补偿模块、二阶泰勒级数补偿模块、正余弦值校正模块等部分组成，在整个结构的实现时采用了流水线结构，这样可以提高数控振荡器的计算速度。图1中灰色的部分是本文提出的对传统CORDIC算法实现的补偿部分。

　　二阶泰勒补偿实现的原理如下：假设相位累加器输出的相角 为N bits的，把相角 分成三部分，即N=j+k+2。由于CORDIC能计算相角的范围为[-99.9°, 99.9°]之间，这是由CORDIC算法本身所决定的，这样就必须通过三角关系把输入相角转换到[-99.9°, 99.9°]之间，本文利用输入相角的高两位来判断相角的转换。然后再把接下的(N-2)bits的数据分成j bits和k bits两部分，中间j bits作为CORDIC的输入相角 ，后k bits作为后续二阶泰勒补偿模块的输入数据。在这里并没有把整个(N-2)bits的角度 作为CORDIC的输入，而是只取了前j bits，这样就会很大程度的降低模块的占用资源，同时，减少输入数据的位宽就会减少迭代的次数。由于这样只取 的高 1位作为CORDIC的输入，这样产生的截断舍入误差会影响到整个数控振荡器的SFDR，为了补偿这部分的损失，本文采取二阶泰勒级数来补偿这部分损失，对于低k bits的角度(-)用来作为二阶泰勒级数补偿的输入相角。利用二阶泰勒级数补偿(公式8)，可以计算出比较准确的正余弦值。

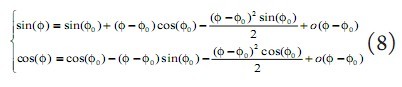
　　仿真结果

　　为了验证结果有可比性，验证性能时采用无杂散动态范围值(SFDR)这一公认指标进行衡量。在频域中，SFDR是衡量一个信号失真特性的有效方法，SFDR为定义在一定频率范围内的信号与第二大频率成分的功率差。在验证性能时，用Matlab对基于CORDIC算法的改进数控振荡器进行仿真，在仿真时采取了定点化仿真，输入相位位数为22bits，输出的正余弦值的位宽为20bits，对于本文提的方法的具体参数设定如下：CORDIC的输入位宽k=10bits，累加器位宽N=22bits，采样频率，输出正余弦信号的频率，仿真的结果如图2(b)所示，从图中可以看出本文提出的方法的SFDR值可以达到114.5dB，输出信号的频谱能量主要集中在10MHz附近，但第二大频率成分的尖峰出现0Hz附近，这个尖峰是未补偿尽残余杂散频谱，它与主频谱幅度相差近115dB，对数控振荡器的性能影响很小。并且，随着累加器位宽和输出信号位宽的增加，数控振荡器的SFDR值会进一步提高，本文的实现方法在输出正余弦值位宽为24bits时，它的SFDR值可以达到134dB。

　　图2(a)所示的是基于传统CORDIC算法实现的数控振荡器，它的SFDR值达到66.5dB。从图2可以看出改进方法提高SFDR值近48dB。本文的改进方法与其他的实现方法的性能比较见表1，从表中可以看出本文提出的改进方法比参考文献提出的实现方法的输出信号SFDR值都要高，所以，本文提出的方法输出信号频谱的纯度要优于其他方法。

　　基于本文设计结构的改进数控振荡器采用了Verilog HDL进行实现，并在Altera公司CycloneⅡ系列的FPGA上进行了综合、布局布线和验证，本设计也在国家“863”项目“软硬件可重构的新一代无线通信统一平台研究”中得到应用，在速度和精度上都能很好的满足平台的需要。

　　结语

　　本文提出一种适用于软件无线电通信系统的数控振荡器实现新方法，该方法利用流水线CORDIC结构来实现数控振荡器，这样可以实现高速的数控振荡器;同时，该方法采用残余相角补偿、二阶泰勒(Taylor)级数近似、相位抖动等措施来补偿CORDIC在精度方面的不足，使数控振荡器的SFDR值得到了很大的提高。该方法实现的数控振荡器能满足软件无线通信系统的速度和精度的要求，并且也成功应用在软件无线电平台上，表现出很好的性能。