摘要:介绍AES中的字节替换算法原理并阐述基于FPGA的设计和实现。为了提高系统工作速度,在设计中应用了流水线技术。最后利用MAXPLUS-II开发工具给出仿真结果,并分析了系统工作速度。
关键词:AES;FPGA;字节替换;流水线技术
1 引言
随着网络技术和无线通信技术的飞速发展,人们对数据传输过程中的安全问题提出了迫切的要求,对于数据加密算述和技术研究也有越来越多的技术人员参与。目前,加密算法按照加密特点分为对称密文和不对密文二大类。AES [1](Advanced Encryption Standard)是NIST(National Institute of Suandard and T echnologies)继2000年10月选择Rijndael算法[2]之后,于2001年11月26日发布的新的对称数据加密算法。
本文首先介绍AES中的SubBytes(字节替换)概貌,并解析出它使用的算法原理,然后论述基于FPGA技术对AES中的字节替换仿真的设计与实现。笔者在运用FPGA技术的过程中完全采用NIST公司的AES算法标准。为了获得在面积和速度上的最佳优化,将流水线设计技术应用到本设计中。另外,本文所得到的仿真结果是在MAXPLUS-II 10.0上运用Verilog HDL硬件描述语言来实现的。
 2 AES中的Subbytes算法描述
AES算法的核心有4种操作[3]:SubTytes(字节替换)、ShiftRows(行位移变换)、MixColumns(列混合变换)和AddRoundKey。这里,主要对SunBytes(字节替换)算法进行描述。
2.1 SunBytes字节替换
字节替换重要的是将一个8位数据转换为另一个不同的8位数据,这里要求一一对应,并且替换结果不能超出8位。例如将00H转换成63H。这个重要的特性正好符合Galois Field(GF)-伽罗瓦域特性。由于转换的数据是8位的,所以符合GF(28)域特性,即GF(28)域中进行的加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF()域加法的最终结果却很简单,GF()加法就是异或(XOR)操作。关于GF()加法和乘法,将在2.3字节中进行描述。
根据NIST描述的ASE算法标准,SunBytes字节替换连续进行以下变换便可达到替换要求。
(1)在GF(28)域中进行乘法变换,即实现多项式m(x)=x8+x4+x3+x+1变换,称之为“multiplicative inverse”。
(2)在GF(28)域中进行交换来实现如下矩阵,称之为“affine transformation”。例如“CA”被变换成“ED”。
2 AES中的Subbytes算法描述
AES算法的核心有4种操作[3]:SubTytes(字节替换)、ShiftRows(行位移变换)、MixColumns(列混合变换)和AddRoundKey。这里,主要对SunBytes(字节替换)算法进行描述。
2.1 SunBytes字节替换
字节替换重要的是将一个8位数据转换为另一个不同的8位数据,这里要求一一对应,并且替换结果不能超出8位。例如将00H转换成63H。这个重要的特性正好符合Galois Field(GF)-伽罗瓦域特性。由于转换的数据是8位的,所以符合GF(28)域特性,即GF(28)域中进行的加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF()域加法的最终结果却很简单,GF()加法就是异或(XOR)操作。关于GF()加法和乘法,将在2.3字节中进行描述。
根据NIST描述的ASE算法标准,SunBytes字节替换连续进行以下变换便可达到替换要求。
(1)在GF(28)域中进行乘法变换,即实现多项式m(x)=x8+x4+x3+x+1变换,称之为“multiplicative inverse”。
(2)在GF(28)域中进行交换来实现如下矩阵,称之为“affine transformation”。例如“CA”被变换成“ED”。
 2.2 在GF(28)域中进行的变换算法
上节所示的二种变换中第二种变换容易实现,而对于第一种变换,假设输入为Y,则输出应为Y-1。在GF(28)域中满足Y255=1[3],所以Y-1=Y-1%26;#183;Y255=Y254。根据这个公式我们就能将求逆变换Y-1转变成在GF(28)域的乘法Y254运算。
图2
2.3 GF(28)域中的加法和乘法
GF(28)域的一个主要特点是加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF(28)域加法的最终结果却很简单。GIF[28]加法即就是异或(XOR)操作。而乘法运算有点繁锁。如果进行乘法运算的二个8位数为A=(a7,a6,a5,a4,a3,a2,a1,a0),B=(b7,b6,b5,b4,b3,b2,b1,b0)。
假设二个多项式为:
A(χ)=a7%26;#183;χ7+a6%26;#183;χ6+a5%26;#183;χ5+a4%26;#183;χ4+a3%26;#183;χ3+a2%26;#183;χ2+a1%26;#183;χ1+a0
B(χ)=b7%26;#183;χ7+b6%26;#183;χ6+b5%26;#183;χ5+b4%26;#183;χ4+b3%26;#183;χ3+b2%26;#183;χ2+b1%26;#183;χ1+b0
C(χ)=A(χ)%26;#215;B(χ)=C14%26;#183;χ14+C13%26;#183;χ13+C12%26;#183;χ12+C11%26;#183;χ11+...
+C114=χ1+C0
C14=a7%26;#183;b7
C13=(a7%26;#183;b6)+(a6%26;#183;b7)
%26;#183;
%26;#183;
C1=(a1%26;#183;b0)+(a0%26;#183;b1)
C0=a0%26;#183;b0
其中:符号“%26;#183;”指的是“与”操作,“+”指的是“异或”操作。
根据GF(28)域特性有
χ8=χ4+χ3+χ+1
χ9...χ14可以根据类型普通乘法运算依次将上式两边同乘以χ得到。这样,可以得到χ14=χ7+χ4+χ3+χ,所以,可以将C(χ)化简成8位多项式:C(χ)=D(χ)=d7χ7+d6χ6+...+d1χ1+d0,具体操作可参考相关文献。
图3
3 FPGA的设计实现
3.1 总体框图
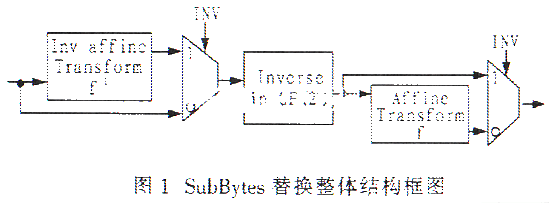
若要在FPGA上实现如上所示的AES字节替换运算,就要运用2.1节所述的二种变换,如图1所示的SunBytes替换整体结构框图,当INV信号为“0”时,输入数据为加密过程,先在GF(28)中进行乘法运算,然后送到GF(2)中进行转换运算;当INV信号为“1”时,输入数据为解密过程,先在GF(2)中进行解密运算,然后计算GF(28)中乘法的逆运算。相应的FPGA实现的具体框图如图2所示。下面,对在FPGA中实现的具体框图进行介绍。
2.2 在GF(28)域中进行的变换算法
上节所示的二种变换中第二种变换容易实现,而对于第一种变换,假设输入为Y,则输出应为Y-1。在GF(28)域中满足Y255=1[3],所以Y-1=Y-1%26;#183;Y255=Y254。根据这个公式我们就能将求逆变换Y-1转变成在GF(28)域的乘法Y254运算。
图2
2.3 GF(28)域中的加法和乘法
GF(28)域的一个主要特点是加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF(28)域加法的最终结果却很简单。GIF[28]加法即就是异或(XOR)操作。而乘法运算有点繁锁。如果进行乘法运算的二个8位数为A=(a7,a6,a5,a4,a3,a2,a1,a0),B=(b7,b6,b5,b4,b3,b2,b1,b0)。
假设二个多项式为:
A(χ)=a7%26;#183;χ7+a6%26;#183;χ6+a5%26;#183;χ5+a4%26;#183;χ4+a3%26;#183;χ3+a2%26;#183;χ2+a1%26;#183;χ1+a0
B(χ)=b7%26;#183;χ7+b6%26;#183;χ6+b5%26;#183;χ5+b4%26;#183;χ4+b3%26;#183;χ3+b2%26;#183;χ2+b1%26;#183;χ1+b0
C(χ)=A(χ)%26;#215;B(χ)=C14%26;#183;χ14+C13%26;#183;χ13+C12%26;#183;χ12+C11%26;#183;χ11+...
+C114=χ1+C0
C14=a7%26;#183;b7
C13=(a7%26;#183;b6)+(a6%26;#183;b7)
%26;#183;
%26;#183;
C1=(a1%26;#183;b0)+(a0%26;#183;b1)
C0=a0%26;#183;b0
其中:符号“%26;#183;”指的是“与”操作,“+”指的是“异或”操作。
根据GF(28)域特性有
χ8=χ4+χ3+χ+1
χ9...χ14可以根据类型普通乘法运算依次将上式两边同乘以χ得到。这样,可以得到χ14=χ7+χ4+χ3+χ,所以,可以将C(χ)化简成8位多项式:C(χ)=D(χ)=d7χ7+d6χ6+...+d1χ1+d0,具体操作可参考相关文献。
图3
3 FPGA的设计实现
3.1 总体框图
若要在FPGA上实现如上所示的AES字节替换运算,就要运用2.1节所述的二种变换,如图1所示的SunBytes替换整体结构框图,当INV信号为“0”时,输入数据为加密过程,先在GF(28)中进行乘法运算,然后送到GF(2)中进行转换运算;当INV信号为“1”时,输入数据为解密过程,先在GF(2)中进行解密运算,然后计算GF(28)中乘法的逆运算。相应的FPGA实现的具体框图如图2所示。下面,对在FPGA中实现的具体框图进行介绍。
 3.2 SENDER模块
该模块每个时钟产生一个0"255的8位二进制数据,用作待加密的明文或待解密的密文。具体程序源代码见SENDER.V。
3.3 AFFINE和INVAFFINE模块
该模块实现了2.1节的第二种变换,对输入数据在GF(28)域中进行矩阵仿射变换。因为要进行的运算比较复杂,在设计中均做了去除毛剌处理,具体框图如图3所示,图中“combinatorial circuit”模块实现GF(28)域的组合逻辑运算,输出有出单元,在CLK的上升沿时刻将处理后的输出寄存到输出级,这样可以达到很好的去除毛剌的效果。在整个设计过程中,均采用这种处理,即在每个模块的输出端均加一个寄存器输出单元。
3.4 AES01模块
该模块实现了2.1节的第一种变换即乘法变换。根据算法要求,该模块在GF(28)域中输入一个8位数据Y,要得到Y-1,因为Y-1=Y-1%26;#183;Y255=Y254,图4可以达到计算Y254的目的。在图4中,2模块对输入数据进行平方运算,X模块对二个输入数据进行乘法运算。平方运算和乘运河运算都符合2.3节所述的乘法运算法则。该模块的运算比较复杂,在FPGA中实现该运算出现很长的路延迟。经过仿真,若将该模块在一个时钟内完成,则最高时钟工作频率只能达到11.13MHz。为了提高系统的工作速度,笔者将流水线技术应用到设计中,如图5所示。
3.2 SENDER模块
该模块每个时钟产生一个0"255的8位二进制数据,用作待加密的明文或待解密的密文。具体程序源代码见SENDER.V。
3.3 AFFINE和INVAFFINE模块
该模块实现了2.1节的第二种变换,对输入数据在GF(28)域中进行矩阵仿射变换。因为要进行的运算比较复杂,在设计中均做了去除毛剌处理,具体框图如图3所示,图中“combinatorial circuit”模块实现GF(28)域的组合逻辑运算,输出有出单元,在CLK的上升沿时刻将处理后的输出寄存到输出级,这样可以达到很好的去除毛剌的效果。在整个设计过程中,均采用这种处理,即在每个模块的输出端均加一个寄存器输出单元。
3.4 AES01模块
该模块实现了2.1节的第一种变换即乘法变换。根据算法要求,该模块在GF(28)域中输入一个8位数据Y,要得到Y-1,因为Y-1=Y-1%26;#183;Y255=Y254,图4可以达到计算Y254的目的。在图4中,2模块对输入数据进行平方运算,X模块对二个输入数据进行乘法运算。平方运算和乘运河运算都符合2.3节所述的乘法运算法则。该模块的运算比较复杂,在FPGA中实现该运算出现很长的路延迟。经过仿真,若将该模块在一个时钟内完成,则最高时钟工作频率只能达到11.13MHz。为了提高系统的工作速度,笔者将流水线技术应用到设计中,如图5所示。
 整个电路可划分为3个流水级,每一级只完成数据处理的一部分,一个时钟周期完成一级数据处理,然后在下一个时钟到来时将处理后的数据传递给下一级;第一组数据进入流水线后,经过一个时钟周期传递到第二级,同时第二级数据进入第一级,数据队列依次前进。每组数据都要经过3个流水线后才能得到最后的计算结果,但是作为整个流水线,每个时钟周期都能计算出一组结果,所以平均计算一组数据只需要一个时钟周期的时间,大大提高了数据处理速度,保证了整个系统以较高的频率工作。经过仿真,最高工作时钟频率可以达到30.21MHz。
3.5 仿真结果
该设计可以满足AES字节替换的要求,并且应用流水线技术使最高时钟工作频率达到30.21MHz,且毛剌现象不严重。
整个电路可划分为3个流水级,每一级只完成数据处理的一部分,一个时钟周期完成一级数据处理,然后在下一个时钟到来时将处理后的数据传递给下一级;第一组数据进入流水线后,经过一个时钟周期传递到第二级,同时第二级数据进入第一级,数据队列依次前进。每组数据都要经过3个流水线后才能得到最后的计算结果,但是作为整个流水线,每个时钟周期都能计算出一组结果,所以平均计算一组数据只需要一个时钟周期的时间,大大提高了数据处理速度,保证了整个系统以较高的频率工作。经过仿真,最高工作时钟频率可以达到30.21MHz。
3.5 仿真结果
该设计可以满足AES字节替换的要求,并且应用流水线技术使最高时钟工作频率达到30.21MHz,且毛剌现象不严重。
编辑: 引用地址:基于FPGA的高级数据加密AES中的字节替换设计
 2 AES中的Subbytes算法描述
AES算法的核心有4种操作[3]:SubTytes(字节替换)、ShiftRows(行位移变换)、MixColumns(列混合变换)和AddRoundKey。这里,主要对SunBytes(字节替换)算法进行描述。
2.1 SunBytes字节替换
字节替换重要的是将一个8位数据转换为另一个不同的8位数据,这里要求一一对应,并且替换结果不能超出8位。例如将00H转换成63H。这个重要的特性正好符合Galois Field(GF)-伽罗瓦域特性。由于转换的数据是8位的,所以符合GF(28)域特性,即GF(28)域中进行的加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF()域加法的最终结果却很简单,GF()加法就是异或(XOR)操作。关于GF()加法和乘法,将在2.3字节中进行描述。
根据NIST描述的ASE算法标准,SunBytes字节替换连续进行以下变换便可达到替换要求。
(1)在GF(28)域中进行乘法变换,即实现多项式m(x)=x8+x4+x3+x+1变换,称之为“multiplicative inverse”。
(2)在GF(28)域中进行交换来实现如下矩阵,称之为“affine transformation”。例如“CA”被变换成“ED”。
2 AES中的Subbytes算法描述
AES算法的核心有4种操作[3]:SubTytes(字节替换)、ShiftRows(行位移变换)、MixColumns(列混合变换)和AddRoundKey。这里,主要对SunBytes(字节替换)算法进行描述。
2.1 SunBytes字节替换
字节替换重要的是将一个8位数据转换为另一个不同的8位数据,这里要求一一对应,并且替换结果不能超出8位。例如将00H转换成63H。这个重要的特性正好符合Galois Field(GF)-伽罗瓦域特性。由于转换的数据是8位的,所以符合GF(28)域特性,即GF(28)域中进行的加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF()域加法的最终结果却很简单,GF()加法就是异或(XOR)操作。关于GF()加法和乘法,将在2.3字节中进行描述。
根据NIST描述的ASE算法标准,SunBytes字节替换连续进行以下变换便可达到替换要求。
(1)在GF(28)域中进行乘法变换,即实现多项式m(x)=x8+x4+x3+x+1变换,称之为“multiplicative inverse”。
(2)在GF(28)域中进行交换来实现如下矩阵,称之为“affine transformation”。例如“CA”被变换成“ED”。
 2.2 在GF(28)域中进行的变换算法
上节所示的二种变换中第二种变换容易实现,而对于第一种变换,假设输入为Y,则输出应为Y-1。在GF(28)域中满足Y255=1[3],所以Y-1=Y-1%26;#183;Y255=Y254。根据这个公式我们就能将求逆变换Y-1转变成在GF(28)域的乘法Y254运算。
图2
2.3 GF(28)域中的加法和乘法
GF(28)域的一个主要特点是加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF(28)域加法的最终结果却很简单。GIF[28]加法即就是异或(XOR)操作。而乘法运算有点繁锁。如果进行乘法运算的二个8位数为A=(a7,a6,a5,a4,a3,a2,a1,a0),B=(b7,b6,b5,b4,b3,b2,b1,b0)。
假设二个多项式为:
A(χ)=a7%26;#183;χ7+a6%26;#183;χ6+a5%26;#183;χ5+a4%26;#183;χ4+a3%26;#183;χ3+a2%26;#183;χ2+a1%26;#183;χ1+a0
B(χ)=b7%26;#183;χ7+b6%26;#183;χ6+b5%26;#183;χ5+b4%26;#183;χ4+b3%26;#183;χ3+b2%26;#183;χ2+b1%26;#183;χ1+b0
C(χ)=A(χ)%26;#215;B(χ)=C14%26;#183;χ14+C13%26;#183;χ13+C12%26;#183;χ12+C11%26;#183;χ11+...
+C114=χ1+C0
C14=a7%26;#183;b7
C13=(a7%26;#183;b6)+(a6%26;#183;b7)
%26;#183;
%26;#183;
C1=(a1%26;#183;b0)+(a0%26;#183;b1)
C0=a0%26;#183;b0
其中:符号“%26;#183;”指的是“与”操作,“+”指的是“异或”操作。
根据GF(28)域特性有
χ8=χ4+χ3+χ+1
χ9...χ14可以根据类型普通乘法运算依次将上式两边同乘以χ得到。这样,可以得到χ14=χ7+χ4+χ3+χ,所以,可以将C(χ)化简成8位多项式:C(χ)=D(χ)=d7χ7+d6χ6+...+d1χ1+d0,具体操作可参考相关文献。
图3
3 FPGA的设计实现
3.1 总体框图
若要在FPGA上实现如上所示的AES字节替换运算,就要运用2.1节所述的二种变换,如图1所示的SunBytes替换整体结构框图,当INV信号为“0”时,输入数据为加密过程,先在GF(28)中进行乘法运算,然后送到GF(2)中进行转换运算;当INV信号为“1”时,输入数据为解密过程,先在GF(2)中进行解密运算,然后计算GF(28)中乘法的逆运算。相应的FPGA实现的具体框图如图2所示。下面,对在FPGA中实现的具体框图进行介绍。
2.2 在GF(28)域中进行的变换算法
上节所示的二种变换中第二种变换容易实现,而对于第一种变换,假设输入为Y,则输出应为Y-1。在GF(28)域中满足Y255=1[3],所以Y-1=Y-1%26;#183;Y255=Y254。根据这个公式我们就能将求逆变换Y-1转变成在GF(28)域的乘法Y254运算。
图2
2.3 GF(28)域中的加法和乘法
GF(28)域的一个主要特点是加法或乘法操作的结果必须在{0x00 ...0xff}这组数中。虽然GF()域论是相当深奥的,但GF(28)域加法的最终结果却很简单。GIF[28]加法即就是异或(XOR)操作。而乘法运算有点繁锁。如果进行乘法运算的二个8位数为A=(a7,a6,a5,a4,a3,a2,a1,a0),B=(b7,b6,b5,b4,b3,b2,b1,b0)。
假设二个多项式为:
A(χ)=a7%26;#183;χ7+a6%26;#183;χ6+a5%26;#183;χ5+a4%26;#183;χ4+a3%26;#183;χ3+a2%26;#183;χ2+a1%26;#183;χ1+a0
B(χ)=b7%26;#183;χ7+b6%26;#183;χ6+b5%26;#183;χ5+b4%26;#183;χ4+b3%26;#183;χ3+b2%26;#183;χ2+b1%26;#183;χ1+b0
C(χ)=A(χ)%26;#215;B(χ)=C14%26;#183;χ14+C13%26;#183;χ13+C12%26;#183;χ12+C11%26;#183;χ11+...
+C114=χ1+C0
C14=a7%26;#183;b7
C13=(a7%26;#183;b6)+(a6%26;#183;b7)
%26;#183;
%26;#183;
C1=(a1%26;#183;b0)+(a0%26;#183;b1)
C0=a0%26;#183;b0
其中:符号“%26;#183;”指的是“与”操作,“+”指的是“异或”操作。
根据GF(28)域特性有
χ8=χ4+χ3+χ+1
χ9...χ14可以根据类型普通乘法运算依次将上式两边同乘以χ得到。这样,可以得到χ14=χ7+χ4+χ3+χ,所以,可以将C(χ)化简成8位多项式:C(χ)=D(χ)=d7χ7+d6χ6+...+d1χ1+d0,具体操作可参考相关文献。
图3
3 FPGA的设计实现
3.1 总体框图
若要在FPGA上实现如上所示的AES字节替换运算,就要运用2.1节所述的二种变换,如图1所示的SunBytes替换整体结构框图,当INV信号为“0”时,输入数据为加密过程,先在GF(28)中进行乘法运算,然后送到GF(2)中进行转换运算;当INV信号为“1”时,输入数据为解密过程,先在GF(2)中进行解密运算,然后计算GF(28)中乘法的逆运算。相应的FPGA实现的具体框图如图2所示。下面,对在FPGA中实现的具体框图进行介绍。
 3.2 SENDER模块
该模块每个时钟产生一个0"255的8位二进制数据,用作待加密的明文或待解密的密文。具体程序源代码见SENDER.V。
3.3 AFFINE和INVAFFINE模块
该模块实现了2.1节的第二种变换,对输入数据在GF(28)域中进行矩阵仿射变换。因为要进行的运算比较复杂,在设计中均做了去除毛剌处理,具体框图如图3所示,图中“combinatorial circuit”模块实现GF(28)域的组合逻辑运算,输出有出单元,在CLK的上升沿时刻将处理后的输出寄存到输出级,这样可以达到很好的去除毛剌的效果。在整个设计过程中,均采用这种处理,即在每个模块的输出端均加一个寄存器输出单元。
3.4 AES01模块
该模块实现了2.1节的第一种变换即乘法变换。根据算法要求,该模块在GF(28)域中输入一个8位数据Y,要得到Y-1,因为Y-1=Y-1%26;#183;Y255=Y254,图4可以达到计算Y254的目的。在图4中,2模块对输入数据进行平方运算,X模块对二个输入数据进行乘法运算。平方运算和乘运河运算都符合2.3节所述的乘法运算法则。该模块的运算比较复杂,在FPGA中实现该运算出现很长的路延迟。经过仿真,若将该模块在一个时钟内完成,则最高时钟工作频率只能达到11.13MHz。为了提高系统的工作速度,笔者将流水线技术应用到设计中,如图5所示。
3.2 SENDER模块
该模块每个时钟产生一个0"255的8位二进制数据,用作待加密的明文或待解密的密文。具体程序源代码见SENDER.V。
3.3 AFFINE和INVAFFINE模块
该模块实现了2.1节的第二种变换,对输入数据在GF(28)域中进行矩阵仿射变换。因为要进行的运算比较复杂,在设计中均做了去除毛剌处理,具体框图如图3所示,图中“combinatorial circuit”模块实现GF(28)域的组合逻辑运算,输出有出单元,在CLK的上升沿时刻将处理后的输出寄存到输出级,这样可以达到很好的去除毛剌的效果。在整个设计过程中,均采用这种处理,即在每个模块的输出端均加一个寄存器输出单元。
3.4 AES01模块
该模块实现了2.1节的第一种变换即乘法变换。根据算法要求,该模块在GF(28)域中输入一个8位数据Y,要得到Y-1,因为Y-1=Y-1%26;#183;Y255=Y254,图4可以达到计算Y254的目的。在图4中,2模块对输入数据进行平方运算,X模块对二个输入数据进行乘法运算。平方运算和乘运河运算都符合2.3节所述的乘法运算法则。该模块的运算比较复杂,在FPGA中实现该运算出现很长的路延迟。经过仿真,若将该模块在一个时钟内完成,则最高时钟工作频率只能达到11.13MHz。为了提高系统的工作速度,笔者将流水线技术应用到设计中,如图5所示。
 整个电路可划分为3个流水级,每一级只完成数据处理的一部分,一个时钟周期完成一级数据处理,然后在下一个时钟到来时将处理后的数据传递给下一级;第一组数据进入流水线后,经过一个时钟周期传递到第二级,同时第二级数据进入第一级,数据队列依次前进。每组数据都要经过3个流水线后才能得到最后的计算结果,但是作为整个流水线,每个时钟周期都能计算出一组结果,所以平均计算一组数据只需要一个时钟周期的时间,大大提高了数据处理速度,保证了整个系统以较高的频率工作。经过仿真,最高工作时钟频率可以达到30.21MHz。
3.5 仿真结果
该设计可以满足AES字节替换的要求,并且应用流水线技术使最高时钟工作频率达到30.21MHz,且毛剌现象不严重。
整个电路可划分为3个流水级,每一级只完成数据处理的一部分,一个时钟周期完成一级数据处理,然后在下一个时钟到来时将处理后的数据传递给下一级;第一组数据进入流水线后,经过一个时钟周期传递到第二级,同时第二级数据进入第一级,数据队列依次前进。每组数据都要经过3个流水线后才能得到最后的计算结果,但是作为整个流水线,每个时钟周期都能计算出一组结果,所以平均计算一组数据只需要一个时钟周期的时间,大大提高了数据处理速度,保证了整个系统以较高的频率工作。经过仿真,最高工作时钟频率可以达到30.21MHz。
3.5 仿真结果
该设计可以满足AES字节替换的要求,并且应用流水线技术使最高时钟工作频率达到30.21MHz,且毛剌现象不严重。
上一篇:未知电路板原理图测绘系统的设计与实现
下一篇:开关电容器现场可编程模拟阵列的频域SPICE仿真
- 热门资源推荐
- 热门放大器推荐

 Verilog HDL数字集成电路设计原理与应用
Verilog HDL数字集成电路设计原理与应用 LM111J/883B
LM111J/883B










 京公网安备 11010802033920号
京公网安备 11010802033920号