摘要:在利用FPGA实现数字信号处理方面,分布式算法发挥着关键作用,与传统的乘积-积结构相比,具有并行处理的高效性特点。详细研究了基于FPGA、采用分布式算法实现FIR数字滤波器的原理和方法,并通过Xilinx ISE在Modelsim下进行了仿真。
关键词:分布式算法 DALUT FPGA FIR
数字滤波器正在迅速地代替传统的由R、L、C元件和运算放大器组成的模块滤波器并且日益成为DSP的一种主要处理环节。FPGA也在逐渐取代ASIC和PDSP,用作前端数字信号处理的运算(如:FIR滤波、CORDIC算法或FFT)。乘累加运算是实现大多数DSP算法的重要途径,而分布式算法则能够大大提高乘累加运算的效能。
1 传统的乘累加结构FIR数字滤波器基本理论
FIR滤波器被称为有限长脉冲响应滤波器,与IIR数字滤波器相对应,它的单位脉冲响应h(n)只有有限个数据点。输入信号经过线性时不变系系统输出的过程是一个输入信号与单位脉冲响应进行线性卷积的过程,即:
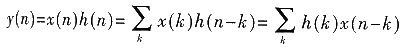 式中,x(n)是输入信号,y(n)是卷积输出,h(n)是系统的单位脉冲响应。可以看出,每次采样y(n)需要进行L次乘法和L-1次加法操作实现乘累加之和,其中L是滤波器单位脉冲响应h(n)的长度。可以发现,当L很大时,每计算一个点,则需要很长的延迟时间。
2 乘累加运算的位宽分配
DSP算法最主要的就是进行乘累加运算。假设采样信号的位宽用N来表示,则N位与N位的乘累结果需要2N位的寄存器来保存;如果两个操作数都是有符号数,则乘积只有2N-1个有效位,因为产生了两个符号位。
为了使累加器的结果不产生溢出,需要对累加器进行冗余设计,也就是说要在累加器2N的位宽上多设计出K位,累加器的长度M计算方式如下(L为滤波器的长度):
对于无符号数:M=2N+K=2N+log2 L
对于有符号数:M=2N=K=2N+log2 L-1
3 乘累加运算的分布式算法原理分析
得益于Xilinx FPGA查找表结构的潜能,分布式算法在滤波器设计方面显示出了很高的效率,自20世纪90年代初以来越来越受到人们的重要。分布式算法是基于查找表的一种计算方法,在利用FPGA实现数字信号处理方面发挥着重要的作用,可以大大提高信号的处理效率。它主要应用于数字滤波、频率转换等数字信号处理的乘累加运算。
分布式算法推导如下:
设Ak是已知常数(如滤波器系数、FFT中的正弦/余弦基本函数等),xk(n)是变量,可以看作是n时刻的第k个采样输入数据,y(n)代表n时刻的系统响应。那么它们的内积为:
式中,x(n)是输入信号,y(n)是卷积输出,h(n)是系统的单位脉冲响应。可以看出,每次采样y(n)需要进行L次乘法和L-1次加法操作实现乘累加之和,其中L是滤波器单位脉冲响应h(n)的长度。可以发现,当L很大时,每计算一个点,则需要很长的延迟时间。
2 乘累加运算的位宽分配
DSP算法最主要的就是进行乘累加运算。假设采样信号的位宽用N来表示,则N位与N位的乘累结果需要2N位的寄存器来保存;如果两个操作数都是有符号数,则乘积只有2N-1个有效位,因为产生了两个符号位。
为了使累加器的结果不产生溢出,需要对累加器进行冗余设计,也就是说要在累加器2N的位宽上多设计出K位,累加器的长度M计算方式如下(L为滤波器的长度):
对于无符号数:M=2N+K=2N+log2 L
对于有符号数:M=2N=K=2N+log2 L-1
3 乘累加运算的分布式算法原理分析
得益于Xilinx FPGA查找表结构的潜能,分布式算法在滤波器设计方面显示出了很高的效率,自20世纪90年代初以来越来越受到人们的重要。分布式算法是基于查找表的一种计算方法,在利用FPGA实现数字信号处理方面发挥着重要的作用,可以大大提高信号的处理效率。它主要应用于数字滤波、频率转换等数字信号处理的乘累加运算。
分布式算法推导如下:
设Ak是已知常数(如滤波器系数、FFT中的正弦/余弦基本函数等),xk(n)是变量,可以看作是n时刻的第k个采样输入数据,y(n)代表n时刻的系统响应。那么它们的内积为:
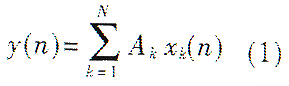 其中,xk(n)变量可以写成下面的格式:
其中,xk(n)变量可以写成下面的格式:
 式中,B为数据格式的字长,xkb是变量的二进制位,只有“0”和“1”两种状态。将(2)式代入(1)式得:
式中,B为数据格式的字长,xkb是变量的二进制位,只有“0”和“1”两种状态。将(2)式代入(1)式得:
 4 FPGA实现过程中查找表的构造方法
根据以上论述,括号中的每一乘积项代表着输入变量的某一位与常量的二进制“与”操作,加号代表着算术和操作,指数因子对括号中的值加权。如果事先构造一个查找表,该表存储着括号中所有可能的组合值,就可以通过所有输入变量相对应位的组合向量(XNb,X(N-1)b,...x1b)对该表进行寻址,该查找表称为DALUT。DALUT的构造规则如表1所示。
4 FPGA实现过程中查找表的构造方法
根据以上论述,括号中的每一乘积项代表着输入变量的某一位与常量的二进制“与”操作,加号代表着算术和操作,指数因子对括号中的值加权。如果事先构造一个查找表,该表存储着括号中所有可能的组合值,就可以通过所有输入变量相对应位的组合向量(XNb,X(N-1)b,...x1b)对该表进行寻址,该查找表称为DALUT。DALUT的构造规则如表1所示。
 5 采用分布式算法实现FIR数字滤波器
为了说明问题,以一个三个系数的FIR数字滤波器为例设计分布式算法,字宽也设置为三位。设FIR数字滤波器系数为:h(0)=5,h(1)=2,h(2)=3。
在进行FPGA设计时,该表以组件Component形式构建,设置为ROM结构,提供输入寻址端口table_in[2..0],输出端口table_out[3..0]。FPGA算法的结构图如图2所示。
5 采用分布式算法实现FIR数字滤波器
为了说明问题,以一个三个系数的FIR数字滤波器为例设计分布式算法,字宽也设置为三位。设FIR数字滤波器系数为:h(0)=5,h(1)=2,h(2)=3。
在进行FPGA设计时,该表以组件Component形式构建,设置为ROM结构,提供输入寻址端口table_in[2..0],输出端口table_out[3..0]。FPGA算法的结构图如图2所示。
 算法实现中的几个关键问题为:
(1)采用状态机实现分布式算法的状态转移
状态机的实现如图3所示,设置三个状态s0、s1、s2 。状态s0完成数据的装入,数据寄存器需要成对出现,一个完成数据的延迟,另一个完成数据的移位,并将状态转移到s1;状态s1完成查找表功能、数据移位和分布式算法的乘累加运算,数据移位一个数据宽带后将状态转移到s2;状态s2完成数据的输出,并将状态转移到s0。利用状态机可以条理清楚地简化计算过程,在算法实现时发挥着关键的作用。
算法实现中的几个关键问题为:
(1)采用状态机实现分布式算法的状态转移
状态机的实现如图3所示,设置三个状态s0、s1、s2 。状态s0完成数据的装入,数据寄存器需要成对出现,一个完成数据的延迟,另一个完成数据的移位,并将状态转移到s1;状态s1完成查找表功能、数据移位和分布式算法的乘累加运算,数据移位一个数据宽带后将状态转移到s2;状态s2完成数据的输出,并将状态转移到s0。利用状态机可以条理清楚地简化计算过程,在算法实现时发挥着关键的作用。
 (2)系统时钟与数据输入时钟的关系
根据上述的状态转移关系,可以得出:每输入一个数据,在下一次数据输入之前,需要在状态s1停留一个数据宽带(三位)的时钟时间,在s2停留一个时钟的数据输出时间。也就是说,系统时钟频率应是数据输入频率的5倍,即fclkock=5fxin。
(3)分布式算法中的乘累加式公推导及核心代表实现
设B是数据的字宽,Pn是分布式算法第n位的结果,则有:
(2)系统时钟与数据输入时钟的关系
根据上述的状态转移关系,可以得出:每输入一个数据,在下一次数据输入之前,需要在状态s1停留一个数据宽带(三位)的时钟时间,在s2停留一个时钟的数据输出时间。也就是说,系统时钟频率应是数据输入频率的5倍,即fclkock=5fxin。
(3)分布式算法中的乘累加式公推导及核心代表实现
设B是数据的字宽,Pn是分布式算法第n位的结果,则有:
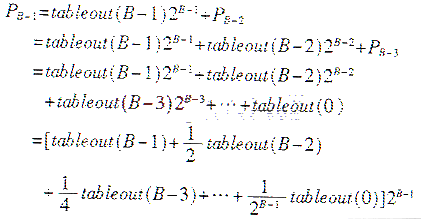 有了该关系式,就可以通过for...loop循环,使用一条语句完成分布式乘累加算法。具体如下:
for n in 0 to B-1 loop
P:=p/2+tableout(n)*2B-1;
End loop;
6 算法仿真验证与结论
本文实现的FIR滤波器在Xilinx的集成开发环境ISE下利用ModelSim进行了仿真。当输入数据为7,3,1...时,仿真输出依次为35,29,32,16...,与乘累加方式FIR滤波算法得出的结果完全一致。假设查找表和PDSP的通用乘法器延时时间相同,分布式算法的等待时间是Br,通用乘法器的等待时间是N1。可见,对于位宽较小的数据来说,分布式算法的执行速度远高于乘累加运算。可见,利用FPGA实现分布式计算大大提高了计算的速度,在高速信号处理中发挥着重要作用。
有了该关系式,就可以通过for...loop循环,使用一条语句完成分布式乘累加算法。具体如下:
for n in 0 to B-1 loop
P:=p/2+tableout(n)*2B-1;
End loop;
6 算法仿真验证与结论
本文实现的FIR滤波器在Xilinx的集成开发环境ISE下利用ModelSim进行了仿真。当输入数据为7,3,1...时,仿真输出依次为35,29,32,16...,与乘累加方式FIR滤波算法得出的结果完全一致。假设查找表和PDSP的通用乘法器延时时间相同,分布式算法的等待时间是Br,通用乘法器的等待时间是N1。可见,对于位宽较小的数据来说,分布式算法的执行速度远高于乘累加运算。可见,利用FPGA实现分布式计算大大提高了计算的速度,在高速信号处理中发挥着重要作用。
编辑: 引用地址:FIR数字滤波器分布式算法的原理及FPGA实现
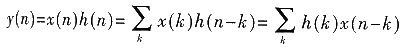 式中,x(n)是输入信号,y(n)是卷积输出,h(n)是系统的单位脉冲响应。可以看出,每次采样y(n)需要进行L次乘法和L-1次加法操作实现乘累加之和,其中L是滤波器单位脉冲响应h(n)的长度。可以发现,当L很大时,每计算一个点,则需要很长的延迟时间。
2 乘累加运算的位宽分配
DSP算法最主要的就是进行乘累加运算。假设采样信号的位宽用N来表示,则N位与N位的乘累结果需要2N位的寄存器来保存;如果两个操作数都是有符号数,则乘积只有2N-1个有效位,因为产生了两个符号位。
为了使累加器的结果不产生溢出,需要对累加器进行冗余设计,也就是说要在累加器2N的位宽上多设计出K位,累加器的长度M计算方式如下(L为滤波器的长度):
对于无符号数:M=2N+K=2N+log2 L
对于有符号数:M=2N=K=2N+log2 L-1
3 乘累加运算的分布式算法原理分析
得益于Xilinx FPGA查找表结构的潜能,分布式算法在滤波器设计方面显示出了很高的效率,自20世纪90年代初以来越来越受到人们的重要。分布式算法是基于查找表的一种计算方法,在利用FPGA实现数字信号处理方面发挥着重要的作用,可以大大提高信号的处理效率。它主要应用于数字滤波、频率转换等数字信号处理的乘累加运算。
分布式算法推导如下:
设Ak是已知常数(如滤波器系数、FFT中的正弦/余弦基本函数等),xk(n)是变量,可以看作是n时刻的第k个采样输入数据,y(n)代表n时刻的系统响应。那么它们的内积为:
式中,x(n)是输入信号,y(n)是卷积输出,h(n)是系统的单位脉冲响应。可以看出,每次采样y(n)需要进行L次乘法和L-1次加法操作实现乘累加之和,其中L是滤波器单位脉冲响应h(n)的长度。可以发现,当L很大时,每计算一个点,则需要很长的延迟时间。
2 乘累加运算的位宽分配
DSP算法最主要的就是进行乘累加运算。假设采样信号的位宽用N来表示,则N位与N位的乘累结果需要2N位的寄存器来保存;如果两个操作数都是有符号数,则乘积只有2N-1个有效位,因为产生了两个符号位。
为了使累加器的结果不产生溢出,需要对累加器进行冗余设计,也就是说要在累加器2N的位宽上多设计出K位,累加器的长度M计算方式如下(L为滤波器的长度):
对于无符号数:M=2N+K=2N+log2 L
对于有符号数:M=2N=K=2N+log2 L-1
3 乘累加运算的分布式算法原理分析
得益于Xilinx FPGA查找表结构的潜能,分布式算法在滤波器设计方面显示出了很高的效率,自20世纪90年代初以来越来越受到人们的重要。分布式算法是基于查找表的一种计算方法,在利用FPGA实现数字信号处理方面发挥着重要的作用,可以大大提高信号的处理效率。它主要应用于数字滤波、频率转换等数字信号处理的乘累加运算。
分布式算法推导如下:
设Ak是已知常数(如滤波器系数、FFT中的正弦/余弦基本函数等),xk(n)是变量,可以看作是n时刻的第k个采样输入数据,y(n)代表n时刻的系统响应。那么它们的内积为:
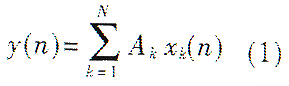 其中,xk(n)变量可以写成下面的格式:
其中,xk(n)变量可以写成下面的格式:
 式中,B为数据格式的字长,xkb是变量的二进制位,只有“0”和“1”两种状态。将(2)式代入(1)式得:
式中,B为数据格式的字长,xkb是变量的二进制位,只有“0”和“1”两种状态。将(2)式代入(1)式得:
 4 FPGA实现过程中查找表的构造方法
根据以上论述,括号中的每一乘积项代表着输入变量的某一位与常量的二进制“与”操作,加号代表着算术和操作,指数因子对括号中的值加权。如果事先构造一个查找表,该表存储着括号中所有可能的组合值,就可以通过所有输入变量相对应位的组合向量(XNb,X(N-1)b,...x1b)对该表进行寻址,该查找表称为DALUT。DALUT的构造规则如表1所示。
4 FPGA实现过程中查找表的构造方法
根据以上论述,括号中的每一乘积项代表着输入变量的某一位与常量的二进制“与”操作,加号代表着算术和操作,指数因子对括号中的值加权。如果事先构造一个查找表,该表存储着括号中所有可能的组合值,就可以通过所有输入变量相对应位的组合向量(XNb,X(N-1)b,...x1b)对该表进行寻址,该查找表称为DALUT。DALUT的构造规则如表1所示。
 5 采用分布式算法实现FIR数字滤波器
为了说明问题,以一个三个系数的FIR数字滤波器为例设计分布式算法,字宽也设置为三位。设FIR数字滤波器系数为:h(0)=5,h(1)=2,h(2)=3。
在进行FPGA设计时,该表以组件Component形式构建,设置为ROM结构,提供输入寻址端口table_in[2..0],输出端口table_out[3..0]。FPGA算法的结构图如图2所示。
5 采用分布式算法实现FIR数字滤波器
为了说明问题,以一个三个系数的FIR数字滤波器为例设计分布式算法,字宽也设置为三位。设FIR数字滤波器系数为:h(0)=5,h(1)=2,h(2)=3。
在进行FPGA设计时,该表以组件Component形式构建,设置为ROM结构,提供输入寻址端口table_in[2..0],输出端口table_out[3..0]。FPGA算法的结构图如图2所示。
 算法实现中的几个关键问题为:
(1)采用状态机实现分布式算法的状态转移
状态机的实现如图3所示,设置三个状态s0、s1、s2 。状态s0完成数据的装入,数据寄存器需要成对出现,一个完成数据的延迟,另一个完成数据的移位,并将状态转移到s1;状态s1完成查找表功能、数据移位和分布式算法的乘累加运算,数据移位一个数据宽带后将状态转移到s2;状态s2完成数据的输出,并将状态转移到s0。利用状态机可以条理清楚地简化计算过程,在算法实现时发挥着关键的作用。
算法实现中的几个关键问题为:
(1)采用状态机实现分布式算法的状态转移
状态机的实现如图3所示,设置三个状态s0、s1、s2 。状态s0完成数据的装入,数据寄存器需要成对出现,一个完成数据的延迟,另一个完成数据的移位,并将状态转移到s1;状态s1完成查找表功能、数据移位和分布式算法的乘累加运算,数据移位一个数据宽带后将状态转移到s2;状态s2完成数据的输出,并将状态转移到s0。利用状态机可以条理清楚地简化计算过程,在算法实现时发挥着关键的作用。
 (2)系统时钟与数据输入时钟的关系
根据上述的状态转移关系,可以得出:每输入一个数据,在下一次数据输入之前,需要在状态s1停留一个数据宽带(三位)的时钟时间,在s2停留一个时钟的数据输出时间。也就是说,系统时钟频率应是数据输入频率的5倍,即fclkock=5fxin。
(3)分布式算法中的乘累加式公推导及核心代表实现
设B是数据的字宽,Pn是分布式算法第n位的结果,则有:
(2)系统时钟与数据输入时钟的关系
根据上述的状态转移关系,可以得出:每输入一个数据,在下一次数据输入之前,需要在状态s1停留一个数据宽带(三位)的时钟时间,在s2停留一个时钟的数据输出时间。也就是说,系统时钟频率应是数据输入频率的5倍,即fclkock=5fxin。
(3)分布式算法中的乘累加式公推导及核心代表实现
设B是数据的字宽,Pn是分布式算法第n位的结果,则有:
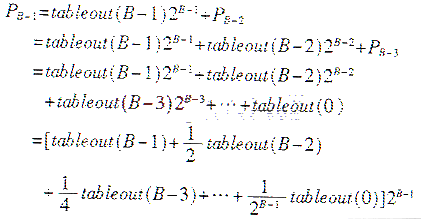 有了该关系式,就可以通过for...loop循环,使用一条语句完成分布式乘累加算法。具体如下:
for n in 0 to B-1 loop
P:=p/2+tableout(n)*2B-1;
End loop;
6 算法仿真验证与结论
本文实现的FIR滤波器在Xilinx的集成开发环境ISE下利用ModelSim进行了仿真。当输入数据为7,3,1...时,仿真输出依次为35,29,32,16...,与乘累加方式FIR滤波算法得出的结果完全一致。假设查找表和PDSP的通用乘法器延时时间相同,分布式算法的等待时间是Br,通用乘法器的等待时间是N1。可见,对于位宽较小的数据来说,分布式算法的执行速度远高于乘累加运算。可见,利用FPGA实现分布式计算大大提高了计算的速度,在高速信号处理中发挥着重要作用。
有了该关系式,就可以通过for...loop循环,使用一条语句完成分布式乘累加算法。具体如下:
for n in 0 to B-1 loop
P:=p/2+tableout(n)*2B-1;
End loop;
6 算法仿真验证与结论
本文实现的FIR滤波器在Xilinx的集成开发环境ISE下利用ModelSim进行了仿真。当输入数据为7,3,1...时,仿真输出依次为35,29,32,16...,与乘累加方式FIR滤波算法得出的结果完全一致。假设查找表和PDSP的通用乘法器延时时间相同,分布式算法的等待时间是Br,通用乘法器的等待时间是N1。可见,对于位宽较小的数据来说,分布式算法的执行速度远高于乘累加运算。可见,利用FPGA实现分布式计算大大提高了计算的速度,在高速信号处理中发挥着重要作用。
上一篇:基于FPGA的毫米波多目标信号形成技术的研究
下一篇:内嵌ARM核的FPGA芯片EPXA10及其在图像驱动和处理方面的应用
- 热门资源推荐
- 热门放大器推荐

 Verilog HDL数字集成电路设计原理与应用
Verilog HDL数字集成电路设计原理与应用 AZ4559M-E1
AZ4559M-E1




 京公网安备 11010802033920号
京公网安备 11010802033920号