|
频率特性又称频率响应,它是指系统或元件对不同频率的正弦输入信号的响应特性。系统的频率特性可由两个方法直接得到:(1) 机理模型—传递函数法;(2) 实验方法。
5.1.1 由传递函数求系统的频率响应
设系统的开环传递函数
对应的频率特性为
如果在S平面的虚轴上任取一点 ,把该点与 ,把该点与 的所有零、极点连接成向量,并将这些向量分别以极坐标的形式表示: 的所有零、极点连接成向量,并将这些向量分别以极坐标的形式表示:
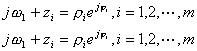
则式(5-3)可改写为
由上式得到其对应的幅值和相角:
同理,可求得对应于 的 的  和 和 。如此继续下去,就能得到一系列幅值和相位与频率 。如此继续下去,就能得到一系列幅值和相位与频率 的关系,其中幅值随频率变化而变化的特性称为系统的幅频特性,相角随频率变化而变化的特性称为系统的相频特性。 的关系,其中幅值随频率变化而变化的特性称为系统的幅频特性,相角随频率变化而变化的特性称为系统的相频特性。
例5-1绘制系统的幅频和相频特性曲线...
设一线性系统的传递函数为
解:传递函数零、极点的分布如图5令  ,代入式(5即当 ,代入式(5即当  时,频率特性的幅值 时,频率特性的幅值  ,相角 ,相角 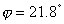 。代入不同的频率 。代入不同的频率  值,重复上述的计算,就可求得对应的一组 值,重复上述的计算,就可求得对应的一组  和 和  值。据此,也可由下面的Matlab 值。据此,也可由下面的Matlab
figure(1),plot(w,x(:)),axis([0,10,0,3]),xlabel('频率(弧度)'),ylabel('幅值');>
figure(2),plot(w,y(:)),axis([0,10,-120,40]),xlabel('频率(弧度)'),ylabel('相角')>
5.1.2 由实验方法求频率特性
系统的频率特性也可用实验方法得到。图5-3给出了一种求取系统频率特性的实验接线方法,它由一台正弦信号发生器、系统或元件装置和双踪示波器组成。信号发生器的频率范围由被测试的实验装置决定,双踪示波器的一路用于测量输出、输入信号的比值,即系统的幅频特性:  ,另一路用于测量输出信号与输入信号的相位差,即系统的相频特性: ,另一路用于测量输出信号与输入信号的相位差,即系统的相频特性: 。通过不断改变输入信号的频率 。通过不断改变输入信号的频率 值,应可以得到系统的频率特性。 值,应可以得到系统的频率特性。
5.1.3 频率特性的基本概念
5.1.3 频率特性的基本概念
线性定常系统的频率特性和时域响应是一致的。在频率特性已知的情况下,可通过数值或解析的方法得到系统的时间响应。
如果一个系统的频率特性已知,则可根据反富里叶级数示取系统的时间响应。令 为控制系统输出的频率特性,则由> 为控制系统输出的频率特性,则由>
>可得到系统输出的时间响应。上面的积分式可通过解析法或根据频特性图由数值法求得。
反过来,若已知系统的时间响应,也可求出系统的频率特性。为了方便理解,下面先以R-C电路为例,并说明频率特性的物理意义。
R-C电路的传递函数为
>设输入电压  ,由复数阻抗的概念求得 ,由复数阻抗的概念求得
如上所述,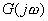 可改写为> 可改写为>
| 式中, |
 , , |
,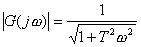 |
 。 。
 称为电路的频率特性。显然,它由该电路的结构和参数决定,与输入信号的幅值和相位无关。 称为电路的频率特性。显然,它由该电路的结构和参数决定,与输入信号的幅值和相位无关。 是 是 的幅值,它表示在稳态时,电路的输出与输入的幅值之比。 的幅值,它表示在稳态时,电路的输出与输入的幅值之比。 是 是 的相角,它表示在稳态时,输出信号与输入信号的相位差。由于 的相角,它表示在稳态时,输出信号与输入信号的相位差。由于 和 和 都是输入信号频率ω的函数,故它们分别被称为电路的幅频特性和相频特性。 都是输入信号频率ω的函数,故它们分别被称为电路的幅频特性和相频特性。
综上所述,式(5—10)所示频率特性的物理意义是:当一频率为ω的正弦信号加到电路的输入端后,在稳态时,电路的输出与输入之比;或者说,电路的输出与输入的幅值之比和相位之差。
根据式(5—9),R-C电路的稳态输出为
由上式可知,当 时,输出与输入的电压不仅幅值相等,而且相位也完全一致。随着ω的不断增大,输出电压的幅值将不断地衰减,相位也不断地滞后。图5—4示出了该电路的幅频和相频特性。 时,输出与输入的电压不仅幅值相等,而且相位也完全一致。随着ω的不断增大,输出电压的幅值将不断地衰减,相位也不断地滞后。图5—4示出了该电路的幅频和相频特性。
同样,对于一般的线性定常系统,设输入为一频率为ω的正弦信号,在稳态时,系统的输出具有和输入同频率的正弦函数,但其幅值和相位一般均不同于输入量,且随着输入信号频率的变化而变化。
设线性系统的传递函数具有式(5-2)的形式,已知输入信号 ,其拉氏变换 ,其拉氏变换  ,A为常量,则系统的输出为 ,A为常量,则系统的输出为
式中,  为 为 的极点。对于稳定系统,这些极点都位于s的左平面,即它们的实部 的极点。对于稳定系统,这些极点都位于s的左平面,即它们的实部 均为负值。为简单起见,令 均为负值。为简单起见,令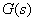 的极点均为相异的实数极点,则式(5—12)改写为 的极点均为相异的实数极点,则式(5—12)改写为
其中 、 、 和 和  (i=1,2,…,n),均为待定系数。对上式取拉氏反变换,求得 (i=1,2,…,n),均为待定系数。对上式取拉氏反变换,求得
当 时,系统响应的瞬态分量 时,系统响应的瞬态分量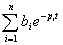 趋向零,其稳态分量为 趋向零,其稳态分量为
其中 、和 、和 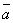 由下列两式确定 由下列两式确定
由于 是一个复数向量,因而可表示为 是一个复数向量,因而可表示为
其中 。注意到式中 。注意到式中 、 、 是ω的偶函数, 是ω的偶函数, 、 、 是ω的奇函数,因而 是ω的奇函数,因而 与 与 互为共轭复数。这样 互为共轭复数。这样  可改写为 可改写为
把式(5—16)~(5—19)代入式(5—15),可得
以上证明了线性定常系统的稳态输出是和输入具有相同频率的正弦信号,其输出与输入的幅值比为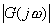 ,输出与输入的相位差 ,输出与输入的相位差 。 。
比较频率特性与传递函数的形式可以发现,只要把传递函数中的 用 用 代之,就可得到系统的频率特性,即有 代之,就可得到系统的频率特性,即有 。可见,频率特性只是传递函数的一种特殊形式,因而它和传递函数一样能表征系统的运动规律,成为描述系统的又一种数学模型。 。可见,频率特性只是传递函数的一种特殊形式,因而它和传递函数一样能表征系统的运动规律,成为描述系统的又一种数学模型。 | 





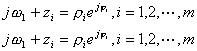



 电子电路识图、应用与检测 (韩雪涛)
电子电路识图、应用与检测 (韩雪涛) 控制之美(卷1)——控制理论从传递函数到状态空间
控制之美(卷1)——控制理论从传递函数到状态空间









 京公网安备 11010802033920号
京公网安备 11010802033920号