当使用双变压器配置时宽带ADC前端设计考虑

变压器用于信号隔离，并且将单端信号转换成差分信号。当在高速模数转换器（ADC）前端电路中使用变压器时常常忽略的一个问题是变压器绝非理想器件。任何由变压器引起的输入失衡都会使输入的正弦信号变成非理想的正弦信号波形传送给ADC的输入端，从而导致ADC的总体性能不如其它方式耦合到ADC的性能。本文讨论了变压器的输入失衡对ADC性能造成的影响，并且提供了实现改进电路的实例。

关于变压器

许多制造商提供的多种多样的型号给变压器选择造成混乱。规定性能的供应商所采用的不同方法将问题复杂化；它们通常在选择和定义他们规定的参数方面都不相同。

当选择一个驱动具体ADC的变压器时应该考虑的几个关键参数是插入损耗、回波损耗、幅度失衡和相位失衡。其中插入损耗表征变压器的带宽能力。回波损耗用于允许用户设计匹配变压器在某个特定频率或频段响应的终端——特别在使用匝 数比大于1的变压器时尤为重要。这里我们集中考虑幅度失衡和相位失衡，以及它们如何影响宽带应用中ADC的性能。

理论分析

即使达到某种宽带额定值，变压器单端输入的原级和差分输出的次级之间的耦合虽然是线性的，但是也会引入幅度失衡和相位失衡。当这些失衡的信号施加到ADC（或其它差分输入器件）时，将加重转换信号（或处理信号）的偶数次失真。虽然这些失衡在低频段对高速ADC引起的附加失真通常可以忽略，但是在频率大约达到100 MHz的高频段变得尤为严重。首先让我们考察一下差分输入信号的幅度和相位失衡（特别是二次谐波失真）如何影响ADC的性能。

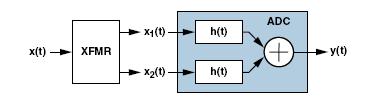
图1：使用变压器耦合的ADC前端简化框图

假设变压器的输入是x(t)。它将被转换为一对信号，x1(t)和x2(t)。如果x(t)是正弦信号? ，则差分输出信号x1(t)和x2(t)形式如下：

x1(t)= k1 sin(ωt)　　　　　　　　　　　　　　　　　(1)

x2(t)= k2 sin(ωt－180°+φ)= －k2 sin(ωt+φ)

ADC的仿真模型为一种对称的三阶传递函数：

h(t)=a0 +a1x(t)+a2x2 (t)+a3x3 (t)　　　　　　　　(2)

则

y(t)=h(x1(t))-h(x2(t))　　　　　　　　　　　　　　　(3)

　y(t)=a1[x1(t)- x2(t)]+a2[x12(t)- x22(t)]+ a3[x13(t)- x23(t)]

理想情况——无失衡

当x1(t)和x2(t)处于理想情况下完全平衡时，它们具有相同的幅度（k1=k2=k），并且相位差严格地相差1800。即

x1(t)=ksin(ωt)　　　　　　　　　　　　　(4)

x2(t)=－ksin(ωt)

y(t) = 2a1ksin(ωt)+ 2a3k3sin3(ωt)　　　　　　(5)

利用三角函数幂指数公式并且整理相同频率项：

这是差分电路的常见的结果：可以消除理想信号的偶次谐波，而不能消除奇次谐波。

幅度失衡

现在假设两个输入信号具有幅度失衡，但没有相位失衡。在这种情况下，k1≠k2, 并且φ＝0。

x1(t)= k1 sin(ωt)　　　　　　　　　　(7)

x2(t)=－k2 sin(ωt)

将公式7带入公式3，并且再次利用三角函数幂指数公式：

我们从公式8中可以看出，这种情况下的二次谐波与幅度值k1和k2的平方差成正比，即

二次谐波∝k12－k22　　　　　　　　　　　（9）

相位失衡

现在假设两个输入信号它们之间具有相位失衡，但没有幅度失衡。那么k1＝k2, 并且φ≠0。

x1(t)= k1 sin(ωt)　　　　　　　　　　　　　(10)

x2(t)＝－k1 sin(ωt+φ)

将公式10带入公式3并且化简，

从公式11，我们可以看出二次谐波的幅度与幅度值k平方成正比。

二次谐波∝k12　　　　　　　　　　　　（12）

结果讨论

比较公式9和公式12可以看出，二次谐波的幅度受相位失衡的影响比受幅度失衡的影响大。对于相位失衡，二次谐波与k1的平方成正比，而对于幅度失衡，二次谐波与k1和k2的平方差成正比。由于k1和k2几乎相等，因此该差值很小。

为了测试这些上述理论计算的有效性，我们为上述模型编写了MATLAB代码以定量和图解说明幅度和相位失衡对采用变压器输入的高性能ADC谐波失真的影响（见附录A）。该模型包括附加的高斯分布白噪声。

MATLAB模型中采用的系数ai用于AD9445高性能125 MSPS 16 bit ADC。图2所示的前端配置中的AD9445用来产生图3所示的快速傅立叶变换（FFT）系数。

图2：采用变压器耦合AD9445的前端配置

图3：AD9445的典型FFT曲线，125 MSPS，IF = 170 MHz

这里的本底噪声、二次谐波和三次谐波反映了ADC和前端电路的复合性能。我们利用这些测量结果计算ADC的失真系数（a2和a3）和噪声，以及在170 MHz输入频率，标准1:1阻抗比率变压器条件下产生的0.0607 dB的幅度失衡和14o的相位失衡。

将这些系数带入公式8和公式11以计算y(t)，而幅度失衡和相位失衡则分别在0 V~1 V和0o～50o（在1 MHz~1000 MHz范围内典型变压器的失衡范围）之间变化，并且观察它们对二次谐波的影响。图4和图5示出其仿真结果。

图4：谐波与幅度失衡的关系曲线

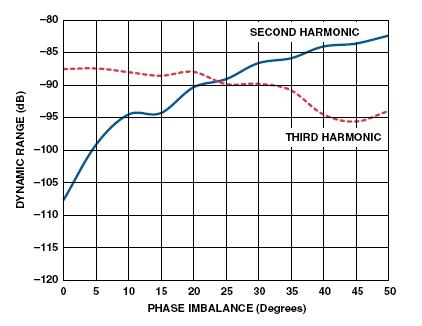
图5：谐波与相位失衡的关系曲线

图4和图5示出(a)三次谐波对于幅度失衡和相位失衡相对不敏感，（b）二次谐波对于相位失衡比幅度失衡恶化得快。因此，为了改善ADC的性能，需要改进引起相位失衡的变压器配置。图6和图7示出两种可行的配置，第一种是双不平衡变压器，第二种是双变压器。

图6：双不平衡变压器

图7：双变压器配置

我们使用专用特性鉴定板上的向量网络分析器比较这两种配置的失衡。图8和图9比较了使用单变压器情况下这两种配置的幅度和相位失衡。

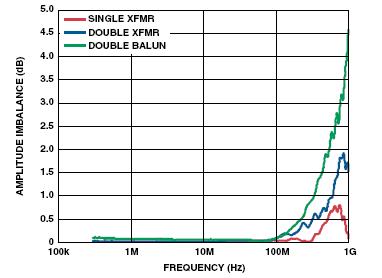
图8：1 MHz~1000 MHz的幅度失衡

图9：1 MHz~1000 MHz的相位失衡

上图清楚地表明双变压器配置以稍微降低幅度失衡为代价改善了相位失衡。因此，利用以上分析结果很明显地看出可利用双变压器配置来提高性能。使用单变压器输入（图10）和双不平衡变压器输入（图11）的AD9445的FFT曲线表明情况确实是这样的；从图中可看出300 MHz中频（IF）信号的SFDR改善了＋10 dB。

图10：单变压器输入的AD9445 FFT曲线，125 MSPS，IF = 300 MHz

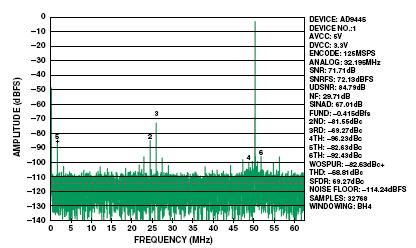
图11：双不平衡变压器耦合的AD9445 FFT曲线，125 MSPS，IF = 300 MHz

这是否意味着为了达到好的性能，我们必须在ADC的前端电路采用两个变压器或者两个不平衡变压器？分析结果表明使用具有很小相位失衡的变压器是必不可少的。在下面的两个实例中（图12和图13），使用两个不同的单变压器来驱动AD9238的170 MHz IF输入信号。这两个实例表明当使用在高频段改进相位失衡的变压器驱动ADC时可将二次谐波改善29 dB。

图12：单变压器耦合的AD9328 FFT曲线，62 MSPS, IF = 170 MHz @ –0.5 dBFS, 二次谐波 = –51.02 dBc

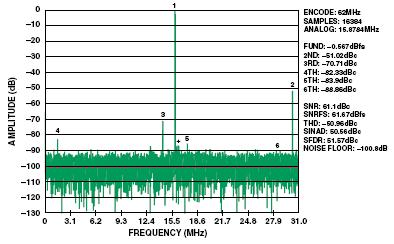
图13：单变压器耦合AD9328 的FFT曲线，62 MSPS, IF = 170 MHz @ –0.5 dBFS, 二次谐波 = –80.56 dBc

结束语

当变压器用作高IF输入（>100 MHz）的处理器（例如ADC、DAC和放大器）时，变压器的相位失衡会加重二次谐波失真。然而，通过使用一对变压器或者不平衡变压器以增加变压器和额外的PCB面积为代价很容易得到显著的改善。

如果设计带宽非常小并且选择了合适的变压器，那么单变压器设计能够达到足够的性能。然而，它们需要有限的带宽匹配，并且可能成本很高或体积很大。

在任何情况下，为任何给定的应用选择最佳的变压器需要对变压器技术指标详细了解。其中相位失衡对于高IF输入（>100 MHz）尤为重要。即使相位失衡在产品使用说明中没有规定，但大部分变压器制造商都应根据要求提供相位失衡信息。如果需要检查或者没有提供相位失衡信息时，可以使用网络分析器来测量变压器的失衡。